14 – Marées
La Terre et la Lune se déplacent en formant un ballet annuel qui tourbillonne et pirouette autour du Soleil. Ensemble, elles font un tour autour du Soleil une fois par an, alors que, dans le même temps, elles virevoltent l’une autour de l’autre faisant un tour tous les 28 jours. La Lune tourne aussi sur elle-même tous les 28 jours, de sorte qu’elle montre toujours la même face à sa partenaire, la Terre. En bonne prima donna, la Terre ne retourne pas le compliment : elle fait sa pirouette une fois par jour. C’est la force de gravité qui perpétue cette danse unie : chaque morceau de Terre, de Lune et de Soleil est attiré vers chaque autre morceau de Terre, de Lune et de Soleil. La somme de toutes ces forces est presque exactement celle qui est nécessaire pour perpétuer ce ballet. Mais il existe des déséquilibres très faibles entre les forces gravitationnelles et les forces nécessaires pour perpétuer cette danse. Ce sont ces déséquilibres qui donnent naissance aux marées.
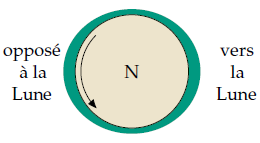
Les déséquilibres qui correspondent au tourbillon de la Lune et de la Terre l’une autour de l’autre sont à peu près trois fois plus importants que les déséquilibres liés à la danse plus lente de la Terre autour du Soleil. Par conséquent, l’amplitude des marées varie avec les phases de la Lune, selon que la Lune et le Soleil sont ou non alignés avec la Terre. Lors de la Pleine Lune et de la Nouvelle Lune (lorsque la Lune, la Terre et le Soleil sont alignés), les déséquilibres se renforcent mutuellement, et les grandes marées qui en résultent sont appelées marées de vives-eaux. (On les appelle aussi parfois « marées d’équinoxe » : à tort, car elles n’arrivent pas au moment de l’équinoxe, mais toutes les deux semaines, aussi régulières qu’une horloge.) A chaque Quartier (le Premier et le Dernier), les déséquilibres se compensent partiellement, et les marées sont plus petites : ce sont des marées de mortes-eaux. Les marées de vives-eaux ont une amplitude environ double des marées de mortes-eaux : l’eau monte deux fois plus haut au dessus de l’altitude moyenne de la surface des mers lors des marées de vives-eaux que lors des marées de mortes-eaux, et les courants de marée y sont également deux fois plus forts.
Pourquoi y a-t-il deux marées hautes et deux marées basses par jour ? Eh bien, si la Terre était une sphère parfaite, une boule de billard lisse recouverte par les océans, l’effet de marée provoqué par le ballet tourbillonnant de la Terre et de la Lune serait de déformer légèrement l’eau dans la direction de la Lune et la direction opposée à la Lune, lui faisant prendre une forme qui ressemble un peu à un ballon de rugby (figure 14.1). Une personne qui vivrait à l’équateur de cette Terre lisse comme une boule de billard, qui fait un tour complet sur elle-même en un jour à l’intérieur de ce cocon aquatique, verrait le niveau de l’eau monter et descendre deux fois par jour : vers le haut une première fois lorsqu’il passe sous le nez du ballon de rugby, et une seconde fois lorsqu’il passe sous sa queue. Cette explication très schématique ne reflète pas totalement la réalité. Dans les faits, la Terre n’est pas lisse, et elle n’est pas uniformément recouverte par de l’eau (peut-être l’avez-vous remarqué). Deux mamelons d’eau ne peuvent pas glisser en faisant le tour de la Terre en une journée parce que sur le passage, il y a des continents. Le véritable comportement des marées est donc bien plus complexe. Dans une grande masse d’eau comme l’océan Atlantique, des bosses et des creux de la marée se forment mais, incapables de glisser tout autour de la Terre, ils font ce qu’ils peuvent, voyageant le long du périmètre de l’océan. Dans l’Atlantique Nord, il y a deux bosses et deux creux qui font le tour de l’Atlantique une fois par jour dans le sens inverse des aiguilles d’une montre. Ici, en Grande-Bretagne, on ne peut pas voir directement ces bosses et ces creux de l’Atlantique — nous sommes en retrait de quelques centaines de kilomètres de la masse principale d’eau océanique, séparés d’elle par une pataugeoire appelée plateau continental. A chaque fois qu’une des bosses de la masse principale atlantique passe devant nous, elle nous envoie une bosse sur notre pataugeoire. De même, chaque creux de l’Atlantique nous envoie un creux sur notre pataugeoire. Les bosses et les creux se suivent avec six heures d’écart. Ou, pour être plus précis, avec six heures et quinze minutes, puisque le délai entre deux levers de Lune est de 25 et non 24 heures.

La vitesse avec laquelle les bosses et les creux voyagent varie avec la profondeur de la pataugeoire. Moins la pataugeoire est profonde, moins les bosses et les creux sont rapides, et plus ils sont grands. En hautemer, les marées ne font que 30 à 50 cm de hauteur. A son arrivée dans les estuaires européens, le marnage (la hauteur entre le niveau de l’eau à marée haute et celui à marée basse) peut aller jusqu’à quatre mètres. Dans l’hémisphère nord, à cause de la force de Coriolis (une force qui correspond à la rotation de la Terre et qui ne s’applique qu’aux objets en mouvement), toutes les bosses et tous les creux de marée ont tendance à serrer le rivage est de la masse d’eau lorsqu’ils se déplacent. Par exemple, les marées de la Manche sont plus importantes du côté français. De même, les bosses et les creux de la mer du Nord près des îles Orcades, au large de la pointe nord-est de l’Écosse, serrent la côte britannique, vont vers l’estuaire de la Tamise, puis tournent ensuite à gauche au niveau des Pays-Bas pour rendre un dernier hommage au Danemark.
L’énergie marémotrice est parfois appelée énergie lunaire, puisque c’est principalement grâce à la Lune que l’eau se balance ainsi. Cependant, l’essentiel de l’énergie marémotrice provient réellement de l’énergie de rotation de la Terre tournant sur elle-même. Et peu à peu, la Terre ralentit.
Donc, comment peut-on rendre utilisable l’énergie des marées, et quelle quantité pourrait-on en tirer ?
Premières estimations de la puissance des marées
Pour exploiter la puissance des marées, on pourrait imaginer un bassin artificiel à côté de la mer, avec une roue à eau qui tourne lorsque le bassin se remplit ou se vide (figures 14.2 et 14.3). Le chapitre G montre comment estimer l’énergie disponible à partir de tels bassins marémoteurs. En supposant que le marnage soit de 4 mètres — une hauteur typique dans de nombreux estuaires européens — la densité de puissance maximum d’un bassin marémoteur artificiel qui se remplit rapidement à marée haute et se vide tout aussi rapidement à marée basse, générant ainsi de la puissance dans les deux directions du courant d’eau, est d’environ 3 W/m2.1 C’est la même puissance par unité de surface que celle obtenue à partir d’un parc éolien offshore. Et nous savons déjà quelle taille les parcs éoliens offshore doivent avoir pour compter vraiment. Ils doivent avoir la taille d’un pays entier. Donc de la même manière, pour faire des bassins marémoteurs qui soient capables de produire une énergie comparable à ce que consomme la Grande-Bretagne, il nous faut une surface totale de bassins marémoteurs du même ordre que la surface de la Grande-Bretagne.
Étonnamment, la Grande-Bretagne est déjà dotée d’un bassin marémoteur naturel aux dimensions requises : la mer du Nord (figure 14.4).2 Si on installait simplement des générateurs dans les lieux appropriés, de la puissance pourrait être extraite dans des quantités significatives. Les générateurs pourraient ressembler à des éoliennes sous-marines. Et parce que la densité de l’eau est 1 000 fois celle de l’air, la puissance du courant d’eau est 1 000 fois plus grande que la puissance du vent à la même vitesse. Nous reviendrons plus loin sur les fermes hydroliennes, mais avant cela, nous allons voir la quantité brute d’énergie de marée qui circule chaque jour autour de la Grande-Bretagne.
| marnage | densité de puissance |
|---|---|
| 2 m | 1 W/m2 |
| 4 m | 3 W/m2 |
| 6 m | 7 W/m2 |
| 8 m | 13 W/m2 |
La puissance brute des marées
Les marées autour de la Grande-Bretagne sont de véritables ondes de marée — contrairement aux tsunamis, que l’on appelle aussi « raz-de-marée », mais qui n’ont absolument rien à voir avec les marées. Suivons une marée haute lorsqu’elle arrive de l’Atlantique. L’heure de la marée haute se décale progressivement dans le temps au fur et à mesure que l’on va vers l’est dans la Manche, de la côte bretonne au Cotentin, puis au Pas-de-Calais. La crête de la vague de marée progresse le long de la Manche à environ 70 km/h. (La bosse de la vague se déplace beaucoup plus vite que l’eau elle-même, tout comme les vagues ordinaires sur la mer se déplacent plus rapidement que l’eau dont sont faites ces vagues.) De même, une marée haute se déplace dans le sens des aiguilles d’une montre autour de l’Écosse, longeant la côte est de la Grande-Bretagne du nord au sud à une vitesse d’environ 100 km/h. Ces deux marées hautes convergent dans l’estuaire de la Tamise. Par coïncidence, la crête écossaise arrive 12 heures après la crête venant de Cornouailles, arrivant de manière presque synchrone avec la marée haute suivante qui vient de Cornouailles, et Londres reçoit ses deux marées hautes classiques par jour.
La puissance que l’on peut extraire des marées ne peut dépasser la puissance totale de ces ondes de marée venant de l’Atlantique. La puissance totale qui croise les lignes de la figure 14.6 a été mesurée : en moyenne, elle s’élève à 100 kWh par jour et par personne.3 Si on imaginait n’extraire que 10 % de cette énergie incidente, en supposant que les processus de conversion et de transmission ont un rendement de 50 %, la puissance moyenne fournie serait de 5 kWh par jour et par personne.
C’est une première estimation grossière, faite sans avoir défini le moindre détail technique. Nous allons maintenant estimer la puissance qui peut être fournie par les trois solutions techniques suivantes : les fermes exploitant le courant de marées (ou fermes hydroliennes), les barrages marémoteurs et les lagons marémoteurs en pleine mer.
Fermes hydroliennes
Une des manières de récupérer l’énergie des courants de marée est de construire des fermes hydroliennes, comme on construit des parcs d’éoliennes. La première turbine de ce genre, ou génératrice de « courant de marée », à être reliée au réseau électrique a été une turbine de « 300 kW », installée en 2003 près de la ville septentrionale de Hammerfest, en Norvège. Aucun résultat détaillé de la production de puissance n’a encore été publié et à ce jour, il n’existe pas encore de ferme hydrolienne avec plus d’une turbine. Il va donc falloir nous reposer sur la physique et un zeste d’intuition pour prévoir combien de puissance ces fermes vont pouvoir produire. En supposant que les règles pour choisir un bon site sont à peu près les mêmes pour le vent et pour les marées, et que le rendement des turbines marémotrices est comparable à celui des meilleures turbines éoliennes, le tableau 14.7 montre la puissance d’une ferme hydrolienne pour quelques vitesses de courant de marée.
Étant donné que des courants de marée de 2 à 3 nœuds sont chose fréquente, il y a de nombreux endroits autour des Îles Britanniques où la puissance par unité de surface d’une ferme hydrolienne serait de 6 W/m2 ou plus. On peut comparer cette densité de puissance à nos estimations concernant les parcs éoliens (2 à 3 W/m2) et photovoltaïques (5 à 10 W/m2).
| vitesse | densité de puissance (W/m2) |
|
|---|---|---|
| (m/s) | (nœuds) | |
| 0.5 | 1 | 1 |
| 1 | 2 | 8 |
| 2 | 4 | 60 |
| 3 | 6 | 200 |
| 4 | 8 | 500 |
| 5 | 10 | 1 000 |
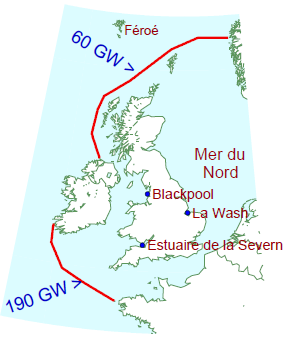
Une puissance des marées pareille, ce serait bête de cracher dessus ! Quelle pourrait être sa contribution, en supposant qu’il n’y ait pas d’obstacle économique à l’exploitation de l’énergie marémotrice sur tous les points chauds autour du Royaume-Uni ? Le chapitre G énumère les vitesses des courants des meilleurs sites britanniques, et estime que 9 kWh/j par personne pourrait en être extraits.
Barrages marémoteurs
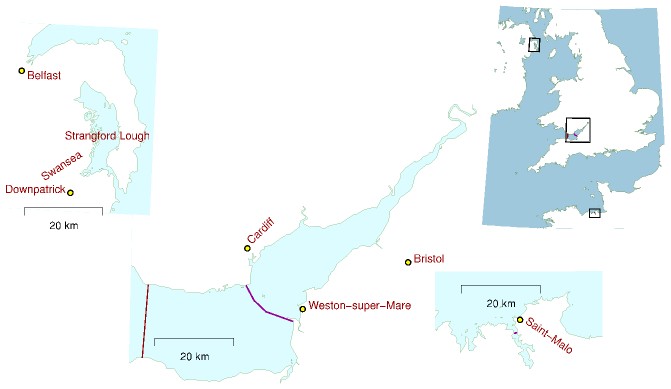
Les barrages marémoteurs sont une technologie éprouvée. Le célèbre barrage de la Rance,4 en Bretagne, où le marnage atteint en moyenne la hauteur record de 8 mètres, produit une puissance moyenne de 60 MW depuis 1966. Le marnage dans l’estuaire de la Severn, à la frontière entre Angleterre et Pays de Galles, est lui aussi exceptionnellement élevé. À Cardiff, le marnage peut atteindre 11,3 mètres en période de vives-eaux, et 5,8 mètres en période de mortes-eaux. Si un barrage était installé en travers de l’embouchure de la Severn (de Weston-super-Mare à Cardiff), il créerait un bassin marémoteur de 500 km2 (figure 14.8). Notez à quel point ce bassin serait beaucoup plus grand que celui de l’estuaire de la Rance. Quelle puissance ce bassin marémoteur pourrait-il offrir, si on laissait l’eau entrer et sortir au bon moment, générant ainsi de la puissance à la fois à marée montante et descendante ? Selon les chiffres théoriques du tableau 14.5, avec un marnage de 11,3 m, la puissance moyenne produite par le barrage (à 30 W/m2) ne dépasserait pas 14,5 GW, soit 5,8 kWh/j par personne. Avec un marnage de 5,8 m, la puissance moyenne apportée par le barrage (à 8 W/m2) serait de 3,9 GW au maximum, soit 1,6 kWh/j par personne. Ces chiffres sont basés sur l’hypothèse qu’on laisse l’eau entrer dans le bassin en une seule vague au moment où la marée est la plus haute, et qu’on la laisse sortir en une seule vague lorsqu’elle est au plus bas. Dans la pratique, l’entrée et la sortie de l’eau seraient étalées sur quelques heures, ce qui réduirait un peu la puissance produite.
Les propositions de barrage actuelles ne produiraient de la puissance que dans une seule direction. Cela réduit encore l’énergie produite de 50 %. Les rapports des ingénieurs portant sur le projet de barrage de la Severn indiquent qu’en ne générant de la puissance qu’en marée descendante, cela fournirait en moyenne 0,8 kWh/j par personne.5 Le barrage offrirait également une protection contre les inondations, évaluée à environ 120 millions de livres sterling par an (150 millions d’euros).
Lagons marémoteurs
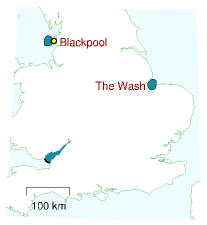
On fabrique des lagons marémoteurs en construisant des murs dans la mer ; les lagons ainsi créés peuvent ensuite être utilisés comme des estuaires artificiels. Cependant, il y a quelques conditions pour pouvoir fabriquer ces lagons : l’eau doit y être peu profonde, et le marnage important. On peut faire des économies d’échelle : l’électricité produite par les lagons marémoteurs est d’autant moins chère que les lagons sont grands. Les deux principaux sites de Grande-Bretagne où l’on pourrait construire de grand lagons marémoteurs sont le Wash sur la côte est et les eaux au large de Blackpool sur la côte ouest (figure 14.9). Des installations plus petites pourraient également être construites dans le nord et le sud-ouest du Pays de Galles, dans le Lincolnshire et dans l’est du Sussex.
Si deux lagons sont construits sur le même site, il y a une astuce que l’on peut utiliser pour augmenter la puissance obtenue et faire que le lagon puisse fournir de la puissance à la demande et à n’importe quel moment, quel que soit l’état de la marée. L’un des lagons peut être défini comme le « lagon supérieur », et l’autre comme le « lagon inférieur ». A marée basse, de la puissance fournie en vidant le lagon supérieur peut être consommée pour vider aussi le lagon inférieur par pompage, et faire que son niveau d’eau soit encore plus bas que la marée basse. L’énergie nécessaire pour vider le lagon inférieur est ensuite remboursée avec intérêts à marée haute, lorsque de la puissance est produite en laissant l’eau entrer dans le lagon inférieur. De même, de l’eau supplémentaire peut être pompée pour surcharger le lagon supérieur à marée haute, en utilisant de l’énergie générée par le lagon inférieur. Quel que soit l’état de la marée, l’un des deux lagons est capable de générer de la puissance. Une telle paire de lagons marémoteurs peut également servir d’installation de stockage d’énergie par pompage, qui emmagasine l’énergie en excès du réseau électrique.
Dans les eaux britanniques, les lagons marémoteurs pourraient produire 4,5 W/m2,6 de puissance moyenne par unité de surface. Donc, si on créait des lagons couvrant en tout 800 km2 (comme indiqué dans la figure 14.9), la puissance générée serait alors de 1,5 kWh/j par personne.
Beautés de la marée
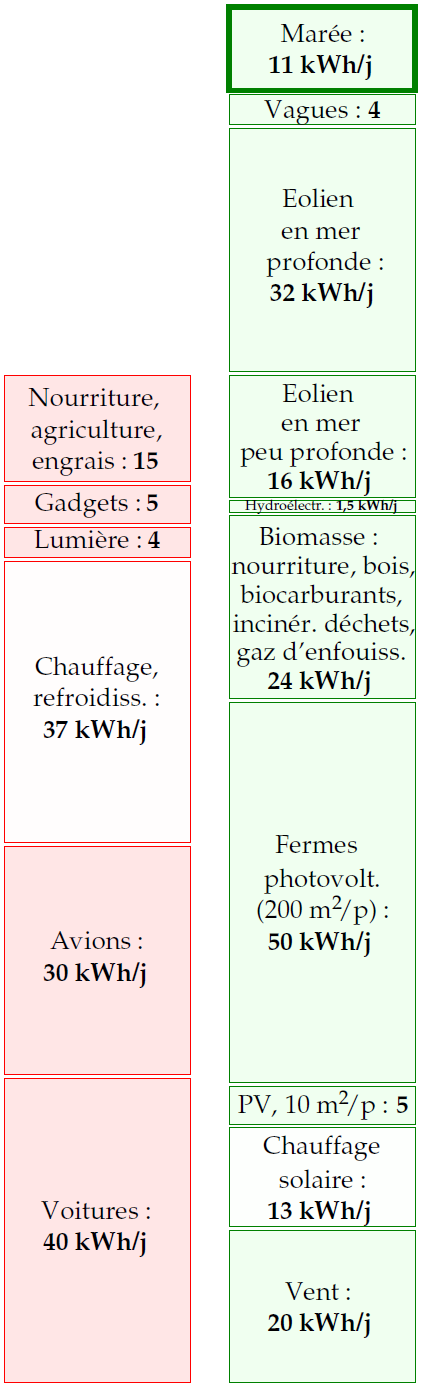
Si on additionne tout, les barrages, les lagons et les fermes exploitant le courant de marée pourraient fournir quelque chose comme 11 kWh/j par personne (figure 14.10).
La puissance des marées n’a jamais été utilisée à l’échelle industrielle en Grande-Bretagne. Il est donc difficile de savoir quels défis économiques et techniques on rencontrerait si l’on construisait et que l’on maintenait des turbines marémotrices — la corrosion, l’envasement, les débris qui s’accumulent ? Mais il y a sept bonnes raisons de s’enthousiasmer pour l’énergie marémotrice dans les Îles Britanniques. 1. L’énergie marémotrice est totalement prévisible. Contrairement à l’éolien et au solaire, l’énergie marémotrice est une énergie renouvelable sur laquelle on pourrait compter ; elle est présente jour et nuit, et toute l’année ; grâce à des lagons marémoteurs, l’énergie peut être stockée afin de fournir de la puissance électrique à la demande. 2. Les marées hautes et basses qui se suivent mettent environ 12 heures à faire le tour des Îles Britanniques. Les courants au large d’Anglesey (Pays de Galles), d’Islay (ouest de l’Écosse), des Orcades (nord-est de l’Écosse) et de Douvres (sud-est de l’Angleterre) sont les plus forts à des moments différents. Par conséquent, prises ensemble, de telles fermes hydroliennes réparties sur ces différents sites pourraient apporter une contribution plus constante à la production électrique qu’une seule ferme hydrolienne prise isolément, même si la production cumulée varie quand même à la hausse et à la baisse au rythme des phases de la Lune. 3. L’énergie marémotrice restera disponible durant des millions d’années. 4. Contrairement à l’énergie photovoltaïque, l’énergie des marées n’impose pas d’utiliser du matériel cher pour être exploitée. 5. En outre, parce que la densité de puissance d’un courant de marée typique est supérieure à celle d’un vent typique, une turbine hydrolienne de 1 MW est plus petite qu’une éolienne de 1 MW. Il n’est donc pas impossible que les turbines marémotrices soient moins chères à fabriquer que les turbines éoliennes de même puissance. 6. La vie sous les vagues est paisible ; les tempêtes de marée, ça n’existe pas. Contrairement aux turbines éoliennes, qui imposent une coûteuse ingénierie pour faire face aux tempêtes de vent rares et violentes, il n’y aura pas besoin de prévoir de gros systèmes de sécurité pour les turbines marémotrices sous l’eau. 7. Les humains vivent pour l’essentiel sur la terre, et ils ne voient pas ce qui se passe sous l’eau. Donc les objections levées du fait de l’impact visuel des turbines marémotrices devraient être bien moins fortes que celles contre les éoliennes.
Légendes urbaines
Toute propre et verte soit-elle, l’énergie marémotrice ne devrait pas être qualifiée de renouvelable. Extraire de l’énergie des marées ralentit la rotation de la Terre. On ne peut absolument pas utiliser l’énergie marémotrice à long terme.
C’est faux. Les marées naturelles ralentissent déjà la rotation de la Terre. La perte naturelle d’énergie de rotation est d’environ 3 TW (Shepherd 2003). Grâce à la friction naturelle des marées, chaque siècle qui passe voit la durée du jour s’allonger de 2,3 millisecondes. De nombreux systèmes de production d’énergie marémotrice ne font qu’extraire de l’énergie qui aurait de toute façon été perdue sous forme de friction. Et même si on multipliait par deux l’énergie extraite du système Terre–Lune, l’énergie marémotrice pourrait encore durer plus d’un milliard d’années.
Notes et bibliographie
↑ 1 La puissance d’un bassin marémoteur artificiel. Une estimation de la puissance par unité de surface d’un bassin marémoteur est calculée dans le chapitre G, page 365.
↑ 2 La Grande-Bretagne est déjà dotée d’un bassin marémoteur naturel … la mer du Nord. Je ne devrais pas donner l’impression que la mer du Nord se vide et se remplit comme un bassin marémoteur sur la côte anglaise. Les courants de la mer du Nord sont plus complexes parce que le temps mis par une bosse d’eau pour se propager le long de la mer est du même ordre que celui qui sépare deux marées. Néanmoins, il existe des courants de marée record entrant et sortant de la mer du Nord, et aussi en son sein.
↑ 3 La puissance totale entrante des ondes de marées lunaires qui croisent ces lignes a été mesurée à 100 kWh par jour et par personne. Source : Cartwright et al. (1980). Pour les lecteurs amateurs de modèles de coin de table, le chapitre G montre comment estimer cette puissance à partir de principes de base.
↑ 4 La Rance a produit 16 TWh en 30 ans, ce qui fait une puissance moyenne de 60 MW (sa puissance crête est de 240 MW). Le marnage peut atteindre 13,5 mètres ; la surface du bassin est de 22 km2 ; le barrage fait 750 mètres de long. Sa densité de puissance moyenne est de 2,7 W/m2. Source : [6xrm5q].
↑ 5 Les rapports des ingénieurs sur la proposition de barrage sur la Severn indiquent … 17 TWh/an. (Taylor, 2002b). Cette puissance (2 GW) correspond, en moyenne, à 5 % de la consommation totale actuelle d’électricité du Royaume-Uni.
↑ 6 La puissance moyenne par unité de surface des bassins marémoteurs pourrait être de 4,5 W/m2. MacKay (2007a).
