G – Marées II
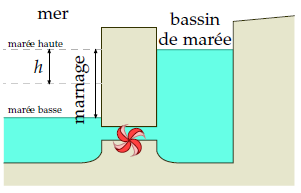
Densité de puissance de lagons marémoteurs
Pour estimer la puissance d’un bassin marémoteur artificiel, imaginons qu’il se remplisse rapidement à marée haute et qu’il se vide rapidement à marée basse. Ses turbines génèrent de la puissance dans les deux sens, à marée montante et descendante. (C’est ce que l’on appelle la génération bidirectionnelle ou à double effet). La variation de l’énergie potentielle de l’eau, toutes les six heures, est égale à mgh, où h est la variation de hauteur du centre de gravité de l’eau, ou amplitude. (L’amplitude est égale à la moitié du marnage, qui est la différence de hauteur entre la marée haute et la marée basse ; figure G.1.) La masse par unité de surface couverte par le bassin marémoteur est égale à ρ × (2h), où ρ est la densité de l’eau (1 000 kg/m3). La puissance par unité de surface générée par un bassin marémoteur est donc égale à :
| 2ρhgh | , |
| 6 heures |
en supposant que les générateurs aient un rendement parfait (100 %). Si l’on intègre une amplitude h = 2 mètres (soit un marnage de 4 mètres), on trouve une puissance par unité de surface de bassin marémoteur de 3,6 W/m2. En se donnant un rendement de conversion de cette puissance en électricité de 90 %,2 on obtient :
puissance par unité de surface de bassin marémoteur ≅ 3 W/m2.
Donc, pour générer 1 GW de puissance (en moyenne), il nous faut un bassin marémoteur couvrant une superficie d’environ 300 km2. Un bassin circulaire d’un diamètre de 20 km ferait l’affaire. (A titre de comparaison, la superficie de l’estuaire de la Severn en amont du barrage actuellement envisagé est d’environ 550 km2, et celle du Wash est supérieure à 400 km2).1
Si un bassin marémoteur ne produit de l’électricité que dans une seule direction, la puissance par unité de surface est réduite de moitié. La densité de puissance moyenne du barrage marémoteur de La Rance, où le marnage est en moyenne de 10,9 mètres, a produit 2,7 W/m2 durant des décennies (page 102).
La ressource marémotrice brute
Les marées autour de la Grande-Bretagne sont d’authentiques vagues de marée. (Les tsunamis, que l’on appelle aussi « raz-de-marée », n’ont rien à voir avec les marées : ils sont provoqués par des glissements de terrain et des tremblements de terre sous-marins). L’onde de marée (ou plus exactement sa crête) se déplace beaucoup plus vite que le flux de marée proprement dit — de l’ordre de 160 kilomètres par heure, alors que l’eau elle-même se déplace à seulement 1 ou 2 kilomètres par heure.
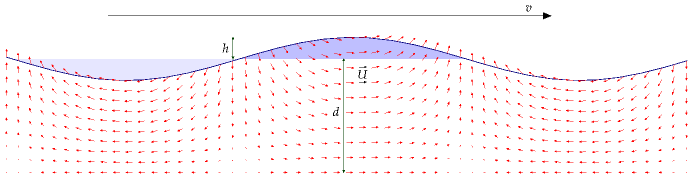
La quantité d’énergie que l’on peut extraire des marées en utilisant des bassins marémoteurs ou des fermes hydroliennes ne pourra jamais être supérieure à la quantité d’énergie que possèdent ces ondes de marée. On peut estimer la puissance totale des grandes ondes de marée de l’océan Atlantique de la même manière que l’on pourrait estimer la puissance de vagues ordinaires générées par le vent. La section qui suit décrit un modèle standard de la puissance qui arrive sous la forme d’ondes qui se propagent dans une eau de profondeur p, lorsque p est faible comparée à la longueur d’onde (figure G.2). La puissance par unité de longueur de crête des ondes de marée en eau peu profonde est de :
ρg3/2√ph2/2.
Le tableau G.3 montre la puissance par unité de longueur de crête d’onde pour quelques valeurs plausibles. Si p = 100 m, et h = 1 mètre (respectivement, h = 2 mètres), la puissance par unité de longueur de crête d’onde est de 150 kW/m (respectivement, de 600 kW/m). Ces chiffres sont impressionnants si on les compare à la puissance brute par unité de longueur des vagues atlantiques ordinaires en eaux profondes, qui est de 40 kW/m (chapitre F). Les vagues et les marées atlantiques ont des amplitudes verticales similaires (environ 1 mètre), mais la puissance brute des marées est environ 10 fois plus grande que celle des vagues ordinaires créées par les vents.
| h (m) |
ρg3/2√ph2/2 (kW/m) |
|---|---|
| 0,9 | 125 |
| 1,0 | 155 |
| 1,2 | 220 |
| 1,5 | 345 |
| 1,75 | 470 |
| 2,0 | 600 |
| 2,25 | 780 |
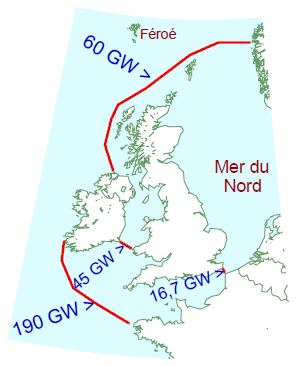
Taylor (1920) a construit un modèle plus détaillé de la puissance des marées, qui prend en compte des détails importants comme la force de Coriolis (l’effet produit par la rotation quotidienne de la Terre), l’existence d’ondes de marées qui se déplacent dans la direction opposée, et l’effet direct de la Lune sur le flux d’énergie dans la mer d’Irlande. Depuis, des mesures expérimentales et des simulations par ordinateur ont vérifié et prolongé l’analyse de Taylor. Flather (1976) a construit un modèle numérique détaillé de la marée lunaire, découpant le plateau continental autour des Îles Britanniques en environ 1 000 cellules carrées. Flather a estimé que la puissance moyenne totale qui arrive dans cette zone était de 215 GW. D’après son modèle, 180 GW entrent dans l’espace qui séparent la France et l’Irlande. De l’Irlande du nord jusqu’aux îles Shetland, la puissance entrante est de 49 GW. Entre les îles Shetland et la Norvège, il y a une perte nette de 5 GW. Comme le montre la figure G.4, Cartwright et al. (1980) ont trouvé de manière expérimentale que la transmission de puissance moyenne était de 60 GW entre Malin Head en Irlande, et Florø en Norvège, et de 190 GW entre Valentia en Irlande et la côte bretonne au large d’Ouessant. La puissance qui entre en mer d’Irlande a été trouvée égale à 45 GW, et celle qui entre en mer du Nord via le Pas de Calais, à 16,7 GW.
La puissance des ondes de marée
Cette section, sur laquelle vous pouvez sans problème faire l’impasse, donne plus de détails sur l’origine de la formule de la puissance des marées utilisée dans la section précédente. Je vais creuser un peu la question parce que les estimations officielles de la ressource marémotrice au Royaume-Uni reposent sur un modèle qui, me semble-t-il, est incorrect.
La figure G.2 montre un modèle d’onde de marée qui se déplace dans une eau relativement peu profonde. Ce modèle permet de schématiser, par exemple, les crêtes d’onde de marée qui remontent la Manche, ou descendent la mer du Nord. Il est important de distinguer la vitesse U à laquelle l’eau elle-même se déplace (qui peut être d’environ 1 ou 2 kilomètres à l’heure) de la vitesse v à laquelle la marée haute se déplace, et qui est typiquement de 200 kilomètres à l’heure.
L’eau a une profondeur p. Les crêtes et les creux d’eau entrent par la gauche du fait des marées océaniques toutes les 12 heures. Ces crêtes et ces creux se déplacent à la vitesse :
v = √gp.
On suppose que la profondeur est très petite par rapport à la longueur d’onde, et on va négliger des détails comme la force de Coriolis et les variations de densité de l’eau de mer. Appelons h l’amplitude verticale de la marée. Du fait de l’hypothèse standard d’un flux quasiment sans tourbillon, la vitesse horizontale de l’eau U est presque constante en fonction de la profondeur. Cette vitesse horizontale est proportionnelle au déplacement en surface, et peut être déterminée par la loi de conservation de la masse :
U = vh/p.
La vitesse de l’onde v diminue avec la profondeur (équation G.2). Pour le moment, on va supposer que la profondeur est constante. L’énergie circule de gauche à droite avec un certain débit. Comment pourrait-on évaluer cette puissance totale de marée ? Et quelle est la puissance maximum qui pourrait en être extraite ?
Une méthode possible consiste à choisir une coupe transversale et à estimer le flux d’énergie cinétique moyen qui traverse cette section plane, puis considérer que cette quantité représente la puissance que l’on pourrait extraire. Cette méthode qui repose sur le flux d’énergie cinétique est celle utilisées par les consultants Black et Veatch pour estimer la ressource marémotrice au Royaume-Uni. Dans notre schéma, on peut calculer la puissance totale d’une autre manière. On va voir que la réponse basée sur le flux d’énergie cinétique sous-estime la ressource d’un facteur multiplicatif significatif.
Le pic du flux d’énergie cinétique dans toute section transversale est égal à :
KBV = 1⁄2ρSU3,
où S est la surface de la section. (Il s’agit de la formule du flux d’énergie cinétique que nous avons rencontrée dans le chapitre B.)
La vraie puissance incidente totale n’est pas égale à ce flux d’énergie cinétique. Le calcul de la vraie puissance incidente totale d’une onde se propageant dans des eaux peu profondes est un classique des livres de cours ; l’une des manières de la déterminer est de calculer la quantité d’énergie totale dans une longueur d’onde et de la diviser par la période. La quantité d’énergie totale par longueur d’onde est la somme de l’énergie potentielle et de l’énergie cinétique. Et il se trouve que l’énergie cinétique est égale à l’énergie potentielle. (Il s’agit d’une caractéristique standard d’à peu près tout ce qui oscille, qu’il s’agisse de masses au bout de ressorts ou d’enfants sur des balançoires). Pour calculer la quantité d’énergie totale, tout ce dont nous avons besoin est donc de calculer l’une des deux quantités d’énergie — soit l’énergie potentielle par longueur d’onde, soit l’énergie cinétique par longueur d’onde — puis de la multiplier par deux. L’énergie potentielle d’une onde (par longueur d’onde et par unité de largeur de front d’onde), se calcule par une intégrale, et vaut :
1⁄4ρgh2λ.
En multipliant ce résultat par deux puis en le divisant par la période, on obtient la véritable puissance de ce modèle d’une onde de marée en eaux peu profondes, qui est égale à :
puissance = 1⁄2(ρgh2λ) × l/T = 1⁄2ρgh2v × l,
où l est la largeur du front d’onde. Et en substituant v = √gp, on obtient :
puissance = ρgh2√gp × l/2 = ρg3/2√ph2 × l/2.
Si, maintenant, on compare cette puissance avec le flux d’énergie cinétique KBV, on remarque quelque chose de frappant : ces deux expressions dépendent d’une puissance différente de l’amplitude h. En utilisant la relation de conversion de l’amplitude (G.3), de la vitesse de la crête d’onde (G.2), et l’égalité S = lp, on peut alors ré-exprimer le flux d’énergie cinétique comme suit :
KBV = 1⁄2ρSU3 = 1⁄2ρlp (vh/p)3 = ρ(g3/2/√p) h3 × l/2.
La méthode du flux d’énergie cinétique suggère donc que la puissance totale d’une onde qui se propage en eaux peu profondes évolue comme le cube de l’amplitude (équation G.8) ; mais la formule correcte montre que la puissance évolue comme le carré de l’amplitude (équation G.7).
Le ratio flux d’énergie cinétique sur puissance est égal à :
| KBV | = | ρl(g3/2/√p) h3 | = | h |
| puissance | ρg3/2h2√pl | p |
Comme hest généralement beaucoup plus petit que p (h est d’environ 1 ou 2 mètres, alors que p est généralement de l’ordre de 100 ou 10 mètres), les estimations de la ressource de puissance de marée qui reposent sur la méthode du flux d’énergie cinétique peuvent être beaucoup trop basses, du moins dans les cas où ce schéma d’ondes de marée en eaux peu profondes est applicable.
De plus, les estimations qui reposent sur la méthode du flux d’énergie cinétique supposent à tort que la puissance totale disponible lors des marées de vives-eaux est huit fois plus importante que celle disponible lors des marées de mortes-eaux, en supposant un rapport deux entre l’amplitude des marées de vives-eaux et celles de mortes-eaux. Mais la réponse correcte est que la puissance totale disponible d’une onde en déplacement évolue comme le carré de l’amplitude de cette onde, et non comme son cube. Le rapport de la puissance totale disponible entre les marées de vives-eaux et de mortes-eaux est donc de quatre.
Effets d’un fond marin en pente et de la force de Coriolis
Si la profondeur p diminue peu à peu et que la largeur reste constante de telle sorte que le rebond et l’absorption de la puissance entrante soient minimaux, alors la puissance de l’onde restera constante. Cela signifie que √ph2 est une constante, ce dont on peut déduire que l’amplitude de la marée varie avec la profondeur en h ≅ 1/p1/4.
Il s’agit un modèle assez grossier. L’un des détails que nous avons négligés, c’est la force de Coriolis. Cette force a pour effet de pousser les crêtes et les creux de marée vers l’est — par exemple, en remontant la Manche, les marées hautes sont plus hautes et les marées basses plus basses sur la côte française que sur la côte britannique. En négligeant cet effet, j’ai pu introduire une petite erreur dans les estimations.
Densité de puissance de fermes marémotrices
Imaginons que l’on installe des turbines sous-marines fixées au fond marin (des hydroliennes). Le flux d’eau va faire tourner ces turbines. La densité de l’eau étant en gros 1 000 fois celle de l’air, la puissance du flux d’eau est 1 000 fois plus importante que la puissance d’un vent de même vitesse.
Quelle puissance des fermes exploitant le courant de marée pourraient-elles extraire ? Un point crucial est de savoir si l’on peut faire la somme des puissances individuelles des turbines lorsqu’elles sont situées les unes à côté des autres au fond de l’eau. Dans le cas du vent, cette hypothèse d’additivité est considérée comme réaliste : du moment que les turbines éoliennes sont écartées les unes des autres d’une distance standard, la puissance totale fournie par 10 fermes éoliennes adjacentes est la somme des puissances que chacune fournirait si elle était isolée.
En va-t-il de même pour les fermes hydroliennes ? Ou bien les hydroliennes interfèrent-elles différemment entre elles ? Je ne crois pas que l’on ait de réponse définitive à cette question, du moins dans le cas général. On peut cependant donner deux hypothèses mutuellement exclusives et identifier des situations schématiques dans lesquelles l’une ou l’autre semble valide. Selon la première hypothèse « la marée fonctionne comme le vent », on peut installer des hydroliennes partout sur le fond de la mer, à condition de les espacer d’environ 5 diamètres les unes des autres, et elles ne se gêneront pas les unes les autres, quelle que soit la surface de fond marin recouverte d’hydroliennes. Par contre, selon la seconde hypothèse « on ne peut installer qu’une seule ligne d’hydroliennes », la puissance maximum extractible dans une zone donnée est la puissance qui serait fournie par une seule ligne de turbines faisant face au flux. Une situation où cette seconde hypothèse se vérifie, c’est le cas particulier d’un barrage hydroélectrique : si l’eau d’un barrage passe à travers une seule turbine bien conçue, ça ne sert à rien d’installer d’autres turbines derrière elle. On ne peut pas obtenir 100 fois plus de puissance en installant 99 turbines supplémentaires en aval de la première ; tout le jus est extrait par la première, et il n’y en a plus pour les suivantes. L’hypothèse « on ne peut installer qu’une seule ligne d’hydroliennes » est donc la bonne lorsqu’il s’agit d’estimer la puissance extractible quand l’eau s’écoule à travers un étroit chenal depuis un bassin d’eau stationnaire à une hauteur donnée vers une autre étendue d’eau de plus faible hauteur. (Ce cas est celui analysé par Garrett et Cummins (2005, 2007).)
Je vais maintenant donner mon avis personnel. Je pense que dans de nombreux endroits autour des Îles Britanniques, l’hypothèse « la marée fonctionne comme le vent » est une bonne approximation. Il y a peut-être quelques sites dont les caractéristiques correspondent à celles d’un chenal étroit, et il est possible que pour ces sites, mes estimations soient surévaluées.
| U | puissance de la | |
|---|---|---|
| (m/s) | (nœuds) | ferme hydrolienne |
| (W/m2) | ||
| 0,5 | 1 | 1 |
| 1 | 2 | 8 |
| 2 | 4 | 60 |
| 3 | 6 | 200 |
| 4 | 8 | 500 |
| 5 | 10 | 1000 |
Supposons que les règles qui s’appliquent pour agencer une ferme hydrolienne raisonnable soient semblables à celles qui s’appliquent aux fermes éoliennes, et que le rendement des hydroliennes soit proche de celui des meilleures éoliennes, soit environ ½. On peut alors emprunter la formule de la puissance d’une ferme éolienne (par unité de surface de terres) de la page 313. La puissance par unité de surface de fond de mer est donc :
| puissance par hydrolienne | = | π | × | 1 | ρU3 |
| superficie par hydrolienne | 200 | 2 |
En utilisant cette formule, le tableau G.6 montre la puissance de cette ferme hydrolienne selon quelques courants de marée.
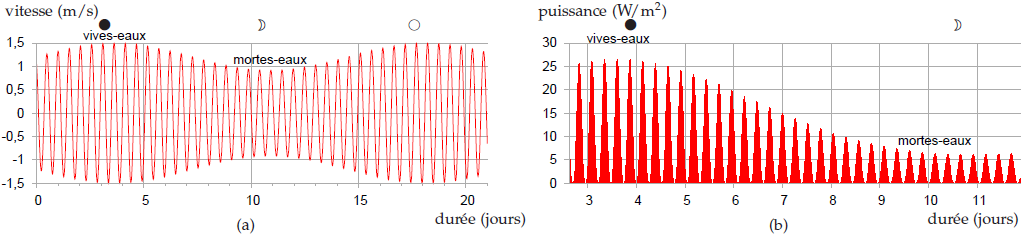
Ceci étant dit, quels sont les courants de marée typiques ? Les annuaires de marée donnent généralement les courants associés aux marées de plus grand marnage (les marées de vives-eaux) et de plus faible marnage (les marées de mortes-eaux). Ces premières ont lieu après chaque pleine lune et chaque nouvelle lune, et ces dernières après chaque premier et dernier quartier. La puissance d’une ferme marémotrice varierait en permanence, mais de manière totalement prévisible. La figure G.5 illustre la manière dont varie la densité de puissance d’une ferme hydrolienne sur un site où le courant maximum est de 1,5 m/s. La densité de puissance moyenne de cette ferme hydrolienne serait de 6,4 W/m2. Il y a de nombreux endroits autour des Îles Britanniques où la puissance par unité de surface de ferme hydrolienne serait d’au moins 6 W/m2. Cette densité de puissance est du même ordre de grandeur que nos estimations des densités de puissance des fermes éoliennes (2 à 3 W/m2) et des fermes photovoltaïques (5 à 10 W/m2).
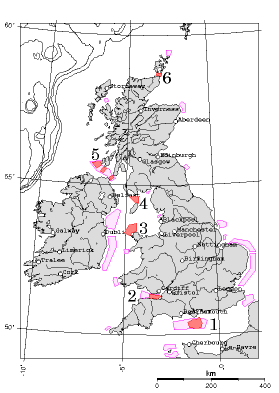
Nous allons maintenant utiliser cette théorie « la marée fonctionne comme le vent » pour estimer la puissance extractible des flux de marée dans les zones prometteuses autour des Îles Britanniques. Par mesure de précaution, nous allons aussi déterminer la puissance totale de marée qui traverse chacune de ces régions en utilisant la théorie de la « puissance des ondes de marée », et nous assurer que notre estimation de la puissance des fermes hydroliennes ne dépasse pas la puissance totale disponible. La figure G.7 montre les principaux sites autour des Îles Britanniques où les courants de marée sont puissants.
J’ai estimé les maxima typiques de courants en six zones où ces courants sont puissants, en consultant un annuaire des marées, le Reed’s Nautical Almanac. (Ces estimations pourraient facilement être fausses de 30 %. Ai-je surestimé ou sous-estimé la superficie de ces zones ? Je n’ai pas étudié en détail la topographie de fonds marins ; je ne sais donc pas si toutes sont entièrement appropriées — certains endroits peuvent être trop profonds, pas assez, ou trop instables.)
| Zone | U | densité | surface | puissance | puiss. brute | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| (nœuds) | de puiss. | moyenne | p | l | M | V | ||||
| M | V | (W/m2) | (km2) | (kWh/j/p) | (m) | (km) | (kWh/j/pers) | |||
| 1 | 1,7 | 3,1 | 7 | 400 | 1,1 | 30 | 30 | 2,3 | 7,8 | |
| 2 | 1,8 | 3,2 | 8 | 350 | 1,1 | 30 | 17 | 1,5 | 4,7 | |
| 3 | 1,3 | 2,3 | 2,9 | 1000 | 1,2 | 50 | 30 | 3,0 | 9,3 | |
| 4 | 1,7 | 3,4 | 9 | 400 | 1,4 | 30 | 20 | 1,5 | 6,3 | |
| 5 | 1,7 | 3,1 | 7 | 300 | 0,8 | 40 | 10 | 1,2 | 4,0 | |
| 6 | 5,0 | 9,0 | 170 | 50 | 3,5 | 70 | 10 | 24 | 78 | |
| Total | 9 | |||||||||
(a)(b)
Une fois ces incertitudes admises, j’arrive à une estimation de puissance totale de 9 kWh/j par personne pour les fermes exploitant les courants de marée. Cela correspond à 9 % de la puissance brute entrante mentionnée en page 98, qui était de 100 kWh par jour et par personne. (Extraire 1,1 kWh/j/pers dans le canal de Bristol, en zone 2, pourrait entrer en conflit avec la production d’énergie par le barrage sur la Severn, selon que la ferme hydrolienne ajoute un frein significatif au frottement naturel préexistant créé par le canal ou le remplace.)
| v (m/s) |
v (nœuds) |
densité de puissance de frottement (W/m2) |
densité de puissance de la ferme hydrolienne |
|
| R1 = 0,01 | R1 = 0,003 | (W/m2) | ||
| 0,5 | 1 | 1,25 | 0,4 | 1 |
| 1 | 2 | 10 | 3 | 8 |
| 2 | 4 | 80 | 24 | 60 |
| 3 | 6 | 270 | 80 | 200 |
| 4 | 8 | 640 | 190 | 500 |
| 5 | 10 | 1250 | 375 | 1000 |
Estimer la ressource marémotrice par la friction sur le fond marin
Une autre manière d’estimer la puissance que peuvent fournir les marées est de calculer la valeur de la puissance déjà dissipée par friction sur le fond marin. Une couche de turbines placées juste au dessus du fond marin pourrait constituer un fond de substitution, opposant à peu près la même résistance au déplacement de l’eau que le véritable fond marin ; elle pourrait donc extraire à peu près la même quantité de puissance que celle que le frottement dissipait, sans changer fondamentalement les flux de marée.
Donc, quelle est la puissance dissipée par « frottement sur le fond » ? Malheureusement, il n’existe pas de modèle simple de friction sur le fond. Celui-ci dépend de la rugosité du fond marin, et du matériau dont il est constitué — et même avec ces informations, la formule correcte à utiliser n’est pas vraiment établie. Selon l’un des modèles les plus utilisés, l’ordre de grandeur de la résistance (force par unité de surface) est en R1ρU2, où U est la vitesse moyenne du flux et R1 est une quantité sans dimension appelée le coefficient de frottement. On peut estimer la puissance dissipée par unité de surface en multipliant la résistance par la vitesse. Le tableau G.9 montre la puissance dissipée sous forme de frottement, R1ρU3, en supposant que R1 = 0,01 ou R1 = 0,003.
Pour des valeurs du coefficient de frottement de cet ordre, cette puissance de frottement est proche de l’estimation de la puissance qu’une ferme hydrolienne fournirait. C’est une bonne nouvelle, car cela suggère que planter une forêt d’hydroliennes au fond de la mer, espacées les unes des autres de cinq diamètres, ne modifiera pas radicalement le flux des marées. La friction naturelle a déjà un effet du même ordre.
Bassins marémoteurs avec pompage
« L’astuce du pompage » augmente artificiellement l’amplitude des marées dans un bassin marémoteur pour amplifier la puissance obtenue. Le coût énergétique du pompage pour injecter plus d’eau dans le bassin à marée haute est remboursé avec intérêts lorsque cette même eau quitte le bassin à marée basse ; de la même manière, de l’eau supplémentaire peut être rejetée par pompage à marée basse, puis admise à nouveau dans le bassin à marée haute. L’astuce du pompage est parfois utilisée à La Rance, ce qui augmente sa génération de puissance nette d’environ 10 % (Wilson et Balls, 1990). Calculons la limite théorique pour cette technologie. Je vais supposer que la génération a un rendement de εg = 0,9 et que le pompage a un rendement de εp = 0,85. Le marnage est égal à 2h. Pour faire simple, je vais aussi supposer que les prix d’achat et de revente de l’électricité sont égaux en toute circonstance, de sorte que le surplus optimal de hauteur b au-dessus de la marée haute (hauteur sur laquelle de l’eau supplémentaire est pompée) est donné par (coût marginal d’un pompage supplémentaire = retour marginal de l’eau supplémentaire) :
b/εp = εg(b + 2h).
Si l’on définit le rendement de l’aller-retour de l’eau ε = εgεp = 76 %, on a :
| b = 2h | ε | . |
| 1 − ε |
Par exemple, avec un marnage de 2h = 4 m et un rendement aller-retour de ε = 76 %, le surplus optimal de hauteur est de b = 13 m. Il s’agit de la hauteur maximum pour laquelle un pompage se justifie si le prix de l’électricité est constant.
Supposons que l’astuce inverse soit utilisée à marée basse. (Cela impose que le bassin fasse 30 mètres de hauteur totale !) La puissance délivrée par unité de surface est alors :
où T est la durée qui s’écoule entre marée haute et marée basse. On peut exprimer ceci comme la densité de puissance maximum possible sans pompage, εg2ρgh2/T, à laquelle on applique le coefficient de surplus :
qui est en gros égal à un facteur 4.
Le tableau G.10 montre la densité de puissance théorique qui pourrait être fournie par pompage. Malheureusement, l’astuce du pompage sera rarement exploité à plein, en raison des contraintes économiques pour la construction du bassin : une exploitation totale du pompage impose une hauteur totale de bassin environ 4 fois plus grande que l’amplitude des marées, et elle multiplie par 4 la puissance fournie. Mais la quantité de matériaux pour construire une digue de hauteur H varie comme H2, ce qui signifie que le coût de construction du mur serait multiplié par bien plus que 4. Cet argent supplémentaire serait sans doute mieux investi dans un agrandissement horizontal plutôt que vertical du bassin marémoteur.
L’astuce du pompage peut néanmoins être utilisé gratuitement, tous les jours pour lesquels l’amplitude de la marée naturelle est plus faible que l’amplitude maximum : de l’eau peut être pompée à marée haute pour monter son niveau jusqu’à la hauteur maximum du bassin. Le tableau G.11 donne la puissance fournie si le surplus de hauteur est fixé à h, c’est à dire si la hauteur du bassin est juste le double de l’amplitude naturelle.
Multiplier par deux l’amplitude naturelle est chose facile lors des marées de mortes-eaux, puisque l’amplitude de ces marées est environ la moitié de celle des marées de vives-eaux. Pomper de l’eau dans le bassin lors des marées de mortes-eaux, de sorte que toute l’amplitude d’une marée de vives-eaux soit exploitée, permet aux marées de mortes-eaux de fournir à peu près deux fois plus de puissance que s’il n’y avait aucun pompage. Un système avec pompage présenterait donc des variations de puissance, toutes les deux semaines, d’un facteur de seulement 2 au lieu de 4.
| amplitude h (m) |
surplus de hauteur b (m) |
puissance avec pompage (W/m2) |
puissance sans pompage (W/m2) |
|---|---|---|---|
| 1,0 | 6,5 | 3,5 | 0,8 |
| 2,0 | 13 | 14 | 3,3 |
| 3,0 | 20 | 31 | 7,4 |
| 4,0 | 26 | 56 | 13 |
| amplitude h (m) |
surplus de hauteur b (m) |
puissance avec pompage (W/m2) |
puissance sans pompage (W/m2) |
|---|---|---|---|
| 1,0 | 1,0 | 1,6 | 0,8 |
| 2,0 | 2,0 | 6,3 | 3,3 |
| 3,0 | 3,0 | 14 | 7,4 |
| 4,0 | 4,0 | 25 | 13 |
Obtenir de la puissance marémotrice « en continu » grâce à deux bassins 3
Voici une idée qui ne manque pas de puissance : prenez deux bassins, que l’on appellera, pour l’un, le « bassin supérieur », et pour l’autre, le « bassin inférieur ». A chaque marée haute, on remplit le « bassin supérieur » ; à marée basse, on vide le « bassin inférieur ». Ces remplissages et vidages successifs peuvent être effectués de manière passive au travers d’écluses, ou bien de manière forcée à l’aide de pompes (en utilisant l’astuce mentionnée précédemment). A chaque fois que de la puissance est requise, on laisse l’eau s’écouler du bassin supérieur au bassin inférieur, ou (ce qui est encore mieux en termes de puissance) entre l’un des bassins et la mer. Le coût en capital d’un système à deux bassins est sans doute plus important du fait des digues supplémentaires à construire ; mais on y gagne énormément parce que la puissance devient disponible en permanence, ce qui veut dire que cette production de puissance peut suivre la demande.

On peut utiliser la puissance générée par le bassin inférieur pour pomper de l’eau supplémentaire de la mer vers le bassin supérieur à marée haute, et, de la même manière exploiter la puissance provenant du bassin supérieur pour abaisser le niveau du bassin inférieur par pompage vers la mer à marée basse. Ce système d’autopompage augmenterait la puissance totale fournie par l’installation sans même avoir besoin d’acheter de l’énergie sur le réseau électrique. Cette solution à deux bassins présente une particularité des plus élégantes : le moment optimal pour pomper l’eau vers le bassin supérieur se trouve être à marée haute, qui s’avère être aussi le meilleur moment pour générer de la puissance grâce au bassin inférieur. Réciproquement, la marée basse est le meilleur moment à la fois pour pomper et vider le bassin inférieur, et pour générer de la puissance grâce au bassin supérieur. Par une simulation simple, j’ai trouvé que sur un site dont le marnage naturel est de 4 mètres, un système à deux bassins peut, avec une planification adéquate du pompage, fournir en continu une puissance de 4,5 W/m2 (MacKay, 2007a). Le niveau d’eau de l’un des bassins est maintenu en permanence au-dessus du niveau moyen de la mer, tandis que le niveau de l’eau dans l’autre bassin est maintenu en permanence en-dessous du niveau moyen de la mer. Cette densité de puissance de 4,5 W/m2 est de 50 % supérieure à la densité de puissance moyenne maximum possible d’un bassin marémoteur ordinaire situé au même endroit (3 W/m2). La puissance stable fournie par ce système de bassins aurait plus de valeur que la puissance intermittente et moins souple d’un bassin marémoteur ordinaire.
Un système à deux bassins pourrait aussi fonctionner comme une installation de stockage par pompage.
Notes et bibliographie
↑ 1 La superficie de l’estuaire de la Severn … est d’environ 550 km2. À titre de comparaison, en France, la rade de Brest, la baie de Douarnenez, le golfe du Morbihan, l’estuaire de la Loire et celui de la Gironde ont des superficies respectives de 180, 385, 115, 217 et 635 km2.
↑ 2 Rendement de 90 %… Les turbines ont un rendement d’environ 90 % lorsque leur charge hydraulique est d’au moins 3,7 mètres de hauteur. Baker et al. (2006).
↑ 3 Obtenir de la puissance marémotrice « en continu » grâce à deux bassins. Il existe une centrale marémotrice à deux bassins à Haishan, sur l’île chinoise de Maoyan. Un générateur unique situé entre les deux bassins, comme montré par la figure G.12(a), fournit de la puissance en continu, et génère en moyenne 39 kW. [2bqapk].
Pour en savoir plus : Shaw et Watson (2003b) ; Blunden et Bahaj (2007) ; Charlier (2003a) ; Charlier (2003b).
Pour en savoir plus sur le frottement de fond et la variation du flux en
fonction de la profondeur, voir Sleath (1984).
Pour en savoir plus sur l’estimation de la ressource marémotrice au Royaume-Uni,
voir MacKay (2007b).
Pour en savoir plus sur les lagons marémoteurs, voir MacKay (2007a).
