E – Chauffage II

Si l’on pouvait construire un bâtiment parfaitement calfeutré et isolé, il retiendrait la chaleur pour toujours et n’aurait donc jamais besoin d’être chauffé. Dans la pratique, les deux principales raisons qui font que les bâtiments perdent de la chaleur sont les suivantes :

La conduction — la chaleur s’écoule directement à travers les murs, les fenêtres et les portes ;
La ventilation — l’air chaud s’infiltre à travers les fissures, les trous, ou les conduits de ventilation intentionnels.

Selon le modèle standard qui décrit les pertes de chaleur, ces deux flux sont proportionnels à la différence de température entre l’air intérieur et extérieur. Pour une maison britannique typique, la conduction constitue la perte principale, comme nous allons le voir maintenant.

Pertes par conduction

Le rythme de conduction de la chaleur à travers un mur, un plafond, un plancher ou une fenêtre, est le produit de trois choses : la surface du mur, une mesure de la conductivité du mur, baptisée dans le jargon « coefficient de transfert global » ou « coefficient U », et la différence de température —

pertes en énergie = surface × U × différence de température.

Le coefficient U est généralement mesuré en W/m²/K. (Un kelvin (1 K) est identique à un degré Celsius (1°C).) Un coefficient U élevé se traduit par des pertes énergétiques élevées. Plus un mur est épais, plus son coefficient U est bas. Un double vitrage est à peu près aussi efficace qu’un mur de briques plein (voir tableau E.1).

Les coefficients U d’objets accumulés les uns contre les autres, comme un mur et son revêtement intérieur, se combinent de la même façon que les conductivités électriques :

Un exemple pratique utilisant cette règle se trouve en page 349.

Pertes par ventilation

Pour pouvoir déterminer la quantité de chaleur qui est nécessaire pour réchauffer l’air froid entrant, il nous faut connaître la capacité thermique de l’air : 1,2 kJ/m³/K.

Tableau E.1. Coefficients U de divers murs, sols, toits et fenêtres.

	Coefficient U (W/m²/K)
	bâti ancien	standards récents	meilleures pratiques
Murs		0,45-0,6	0,12
Mur en maçonnerie solide	2,4
Mur extérieur : brique solide, 22 cm	2,2
Mur creux en parpaings de 28 cm	1,0
Mur isolé en parpaings de 28 cm	0,6
Planchers		0,45	0,14
suspendu en bois	0,7
dalle en béton	0,8
Toits		0,25	0,12
Toit horizontal, 25 mm d’isolation	0,9
Toit en pente, 100 mm d’isolation	0,3
Fenêtres			1,5
Simple vitrage	5,0
Double vitrage	2,9
Double vitrage, espace 20 mm	1,7
Triple vitrage	0,7-0,9

Cuisine	2
Salle de bain	2
Salon	1
Chambre	0,5

Tableau E.2. Renouvellement d’air par heure : valeurs typiques de N pour des pièces correctement calfeutrées. Les pièces avec les pires courants d’air ont N = 3 changements d’air par heure. Le taux de renouvellement minimum recommandé est entre 0,5 et 1,0 renouvellement complet d’air par heure, ce qui fournit suffisamment d’air frais pour la santé humaine, pour brûler des combustibles en sécurité, et pour éviter les dégâts aux éléments du bâtiment qui pourraient résulter d’un excès d’humidité dans l’air (EST 2003).

Dans le métier du bâtiment, on a l’habitude de décrire les pertes provoquées par la ventilation dans un volume donné comme le produit du rythme de renouvellement horaire de l’air N, du volume V en mètres cubes, de la capacité thermique C, et de la différence de température ΔT entre l’intérieur et l’extérieur du bâtiment.

(E.1)

(E.2)

(E.3)

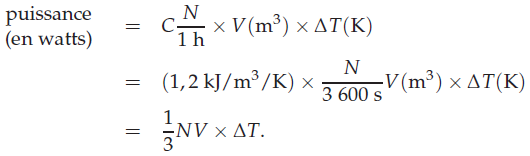
Pertes en énergie et demande en température (degrés-jours)

Puisque l’énergie est la puissance × le temps, on peut écrire l’énergie perdue par conduction à travers une surface sur une courte durée comme :

énergie perdue = surface × U × (ΔT × durée),

et l’énergie perdue par ventilation comme :

¹⁄₃ NV × (ΔT × durée).

Ces deux pertes en énergie ont la forme :

Quelque chose × (ΔT × durée),

Figure E.3. Coefficients U exigés par la réglementation de la construction britannique et suédoise.

où le « Quelque chose » se mesure en watts par °C. Quand la nuit succède au jour, et au fil des saisons, la différence de température ΔT change ; on peut considérer une longue période en la fractionnant en de nombreux petits intervalles de temps, pendant chacun desquels la différence de température est à peu près constante. D’un intervalle de temps à un autre, la différence de température change, mais les Quelques choses ne changent pas. Si l’on cherche à prévoir les pertes d’énergie cumulées par conduction et par ventilation sur un site donné et sur une longue période de temps, il nous faut donc multiplier deux choses :

la somme de tous les Quelques choses (en additionnant surface × U pour tous les murs, plafonds, planchers, portes et fenêtres, et ¹⁄₃ NV pour le volume) ; et
la somme de toutes les facteurs Différence de température × durée (pour tous les intervalles de temps).

Figure E.4. La demande en température à Cambridge, en 2006, visualisée comme une surface sur un graphique des températures moyennes quotidiennes.
(a) Thermostat réglé à 20°C, y compris pour refroidir en été ;
(b) Thermostat réglé à 17°C en hiver.

Le premier facteur est une propriété du bâtiment mesurée en watts par degré Celsius. Je l’appellerai la déperdition du bâtiment (on parle parfois de coefficient de déperdition thermique du bâtiment). Le second facteur est une propriété du temps qu’il fait ; elle est souvent exprimée en « degrés-jours », puisque la différence de température se mesure en degrés, et que les jours sont une unité pratique pour raisonner sur des durées. Par exemple, si l’intérieur de votre maison est à 18°C, et si la température extérieure est de 8°C pendant une semaine, alors on dit que cette semaine a apporté 10 × 7 = 70 degrés-jours à la somme (ΔT × durée). J’appellerai la somme de tous les facteurs (ΔT × durée) la demande en température d’une période.

Figure E.5. Demande en température à Cambridge, en degrés-jours par an, en fonction du réglage du thermostat (°C). Baisser le thermostat en hiver de 20°C à 17°C réduit de 30 % la demande en température pour le chauffage, qui passe de 3 188 à 2 265 degrés-jours. Monter le thermostat en été de 20°C à 23°C réduit de 82 % la demande en température pour la climatisation, qui passe de 91 à 16 degrés-jours.

énergie perdue = déperdition × demande en température.

Nous pouvons réduire nos pertes d’énergie en diminuant la déperdition du bâtiment, ou en réduisant la demande en température, ou les deux. Les deux sections suivantes examinent de plus près ces deux facteurs, en prenant comme sujet d’étude une maison à Cambridge.

Il y a un troisième facteur dont il nous faut aussi parler. L’énergie perdue est remplacée par les systèmes de chauffage du bâtiment, et par d’autres sources d’énergie tels que les occupants, leurs gadgets, leurs appareils de cuisson, et le soleil. Si l’on se focalise sur le système de chauffage, l’énergie que celui-ci fournit n’est pas identique à l’énergie qu’il consomme. Ces deux valeurs sont reliées entre elles par le coefficient de performance du système de chauffage.

énergie consommée = énergie fournie/coefficient de performance.

Pour une chaudière à condensation fonctionnant au gaz naturel, par exemple, le coefficient de performance est de 90 %, parce 10 % de l’énergie part dans la cheminée.

En résumé, on peut réduire la consommation d’énergie d’un bâtiment de trois manières :

en réduisant la demande en température ;
en réduisant la déperdition ; ou
en augmentant le coefficient de performance.

Nous allons maintenant quantifier le potentiel de chacune de ces possibilités. (Une quatrième possibilité — qui consiste à augmenter les gains en chaleur du bâtiment venant de l’extérieur, notamment du soleil — peut aussi être utile, mais je ne la traiterai pas ici.)

La demande en température

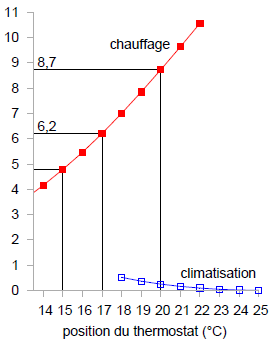
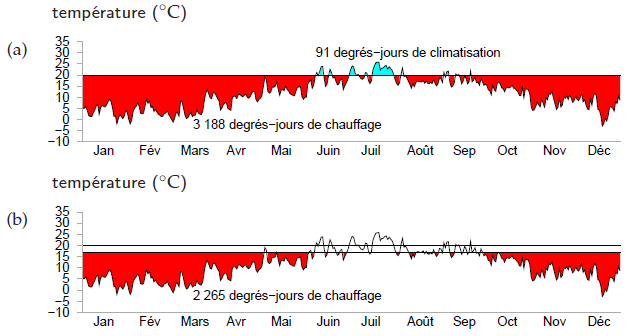
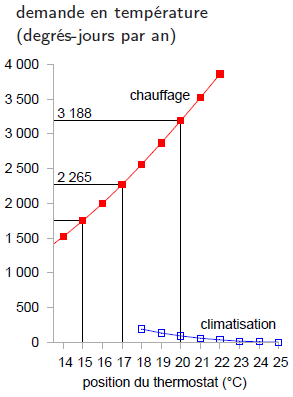
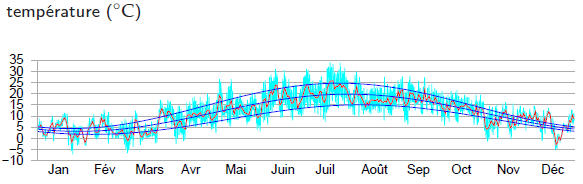
Figure E.6. La demande en température à Cambridge, en 2006, retracée en degrés-jours par jour, autrement dit en degrés. Dans cette unité, la demande en température est simplement la moyenne de la différence de température entre l’intérieur et l’extérieur.

On peut visualiser aisément la demande en température sur un graphique présentant la température extérieure en fonction du temps (figure E.4). Pour un bâtiment maintenu à une température de 20°C, la demande en température totale est la surface entre la ligne horizontale à 20°C et la température extérieure. Sur la figure E.4a, on constate que, pour une année entière, à Cambridge, maintenir une température de 20°C induit une demande en température de 3 188 degrés-jours de chauffage et de 91 degrés-jours de rafraîchissement. Ces graphiques nous permettent facilement d’estimer l’effet d’une baisse du thermostat et de l’absence de climatisation. En baissant le thermostat à 17°C pendant l’hiver, la demande en température pour le chauffage chute de 3 188 degrés-jours à 2 265 degrés-jours (figure E.4b), ce qui correspond à une réduction de 30 % de demande en chauffage. En baissant le thermostat à 15°C, la demande en température passe de 3 188 degrés-jours à 1 748 degrés-jours, soit une réduction de 45 %.

Ces calculs nous donnent une indication grossière de ce que l’on gagne en baissant le thermostat, mais cela ne nous en donnera une prévision exacte qu’à condition de prendre en compte deux éléments supplémentaires : tout d’abord, les bâtiments absorbent naturellement l’énergie qui provient du Soleil, ce qui rend la température intérieure plus élevée que la température extérieure, même en absence de tout chauffage ; ensuite, les occupants et leurs gadgets émettent de la chaleur, ce qui réduit d’autant plus les besoins en chauffage artificiel. La demande en température d’un lieu donné, exprimée de façon conventionnelle en degrés-jours, n’est pas très pratique à manipuler. Pour ma part, j’ai du mal à me rappeler des chiffres tels que « 3 500 degrés-jours ». On peut rendre cette quantité plus intelligible et peut-être plus facile à utiliser en la divisant par 365, qui est le nombre de jours dans l’année : on obtient alors la demande en température exprimée en « degrés-jours par jour » ou, si vous préférez, en « degrés », tout simplement. La figure E.6 nous montre cette demande en température retracée. Exprimée ainsi, la demande en température est simplement la moyenne de la différence de température entre l’intérieur et l’extérieur. Les demandes en température soulignées sont : 8,7°C, pour un thermostat réglé à 20°C ; 6,2°C, pour un réglage à 17°C ; et 4,8°C, pour un réglage à 15°C.

Tableau E.7. Analyse des déperditions de ma maison par conductivité et par ventilation, avant 2006.
J’ai traité le mur séparateur de la maison mitoyenne comme un mur parfaitement isolé, mais cette hypothèse pourrait être fausse dans le cas où l’espace entre maisons adjacentes est bien ventilé.
J’ai fait ressortir les paramètres sur lesquels j’ai agi après 2006, grâce à des modifications que je décrirai plus loin.

Déperdition par conduction	surface (m²)	coefficient U (W/m²/°C)	déperdition (W/°C)
Surfaces horizontales
Toit en pente	48	0,6	28,8
Toit horizontal	1,6	3	4,8
Plancher	50	0,8	40
Surfaces verticales
Murs d’extension	24,1	0,6	14,5
Murs principaux	50	1	50
Murs fins (8 cm)	2	3	6
Portes & fenêtres, simple vitrage	7,35	5	36,7
Fenêtres, double vitrage	17,8	2,9	51,6
Déperdition totale par conduction			232,4

Déperdition par ventilation	volume (m³)	N (renouv. d’air par heure)	déperdition (W/°C)
Chambres	80	0,5	13,3
Cuisine	36	2	24
Hall d’entrée	27	3	27
Autres pièces	77	1	25,7
Déperdition totale par ventilation			90

La déperdition — à travers un exemple, ma maison

Ma maison est un pavillon mitoyen avec trois chambres bâti vers 1940 (figure E.8). En 2006, la cuisine a été un peu agrandie, et la plupart des fenêtres ont reçu un double vitrage. Les portes avant et arrière étaient encore toutes les deux en simple vitrage.

Le tableau E.7 montre le résultat de mon estimation de la déperdition thermique de ma maison, faite en 2006. La déperdition totale était de 322 W/°C (ou 7,7 kWh/j/°C), dont 72 % étaient dus à la déperdition par conduction, et 28 % à la déperdition par ventilation. La déperdition par conduction est divisée en trois parties à peu près égales : les fenêtres ; les murs ; le sol et le plafond.

Figure E.8. Ma maison.

Pour comparer la déperdition de deux bâtiments avec des surfaces au sol différentes, on peut diviser la déperdition par la surface au sol ; cela nous donne le paramètre de pertes thermiques du bâtiment, que l’on mesure en W/°C/m². Le paramètre de pertes thermiques de cette maison (qui a une surface totale au sol de 88 m²) est de :

3,7 W/°C/m².

Utilisons maintenant ces chiffres pour estimer la consommation d’énergie quotidienne de la maison, durant une froide journée d’hiver, et sur l’année entière.

Par un jour froid, en supposant que la température extérieure soit de −1°C et que la température intérieure soit de 19°C, la différence de température est alors égale à ΔT = 20°C. Si cette différence est maintenue pendant 6 heures par jour, alors l’énergie perdue par jour est de :

322 W/°C × 120 degrés-heures ≅ 39 kWh.

Si la température est maintenue à 19°C 24 heures sur 24, l’énergie perdue par jour est de :

155 kWh/j.

Pour obtenir un chiffre de pertes de chaleur sur l’année entière, on peut prendre la demande en température de Cambridge de la figure E.5. Avec un thermostat à 19°C, la demande en température en 2006 était de 2 866 degrés-jours. Le taux moyen de pertes de chaleur, si la maison est toujours gardée à 19°C, est donc de :

7,7 kWh/j/°C × 2 866 degrés-jours/an/(365 jours/an) = 61 kWh/j.

En baissant le thermostat à 17°C, le taux moyen de pertes de chaleur chute à 48 kWh/j. En le montant à une température tropicale de 21°C, les pertes moyennes de chaleur sont de 75 kWh/j.

Résultats d’une isolation plus poussée

Durant l’année 2007, j’ai apporté les modifications suivantes à la maison :

Isolation des cavités murales (ce qui manquait pour les murs principaux de la maison) — figure 21.5.
Augmentation de l’isolation du toit.
Ajout d’une nouvelle porte d’entrée à l’extérieur de l’ancienne porte — figure 21.6.
Remplacement de la porte arrière par une porte avec double vitrage.
Pose d’un double vitrage sur la seule fenêtre qui avait encore un simple vitrage.

Quel changement peut-on prévoir concernant les pertes de chaleur ?

La déperdition totale avant les changements était de 322 W/°C.

L’ajout de l’isolation des cavités murales (nouveau coefficient U de 0,6) aux murs principaux réduit la déperdition de la maison de 20 W/°C. L’isolation améliorée du grenier (nouveau coefficient U de 0,3) devrait réduire la déperdition de 14 W/°C. Les modifications du vitrage (nouveau coefficient U de 1,6 à 1,8) devrait réduire la déperdition par conduction de 23 W/°C, et la déperdition par ventilation de quelque chose comme 24 W/°C. En tout, cela fait une réduction de la déperdition de 25 %, qui passe en gros de 320 à 240 W/°C (de 7,7 à 6 kWh/j/°C). Le tableau E.9 indique les économies prévues pour chaque modification.

Le paramètre de pertes thermiques de cette maison (d’une surface totale au sol de 88 m²) est donc en principe réduit d’environ 25 %, passant de 3,7 à 2,7 W/°C/m. (On est encore loin des 1,1 W/°C/m² requis pour une maison « durable » selon le nouveau code de la construction en Grande-Bretagne.)

Que la difficulté de réduire sérieusement les déperditions d’une maison déjà construite peut être frustrante ! Comme on l’a vu précédemment, il existe un moyen beaucoup plus facile de réduire sérieusement les pertes de chaleur : il suffit de baisser le thermostat. Le baisser de 20 à 17 °C donnait une réduction de 30 % des pertes de chaleur.

Si l’on combine ces deux actions — les modifications physiques et la baisse du thermostat — ce modèle prévoit que les pertes en chaleur devraient baisser de près de 50 %. Dans la mesure où l’ensoleillement, les gadgets et les humains génèrent de la chaleur dans une maison, la baisse de la consommation de gaz devrait même être supérieure à 50 %.

J’ai apporté tous ces changements à ma maison et j’ai regardé mes compteurs chaque semaine. Je peux confirmer que ma facture de chauffage a effectivement baissé de plus de 50 %. Comme le montrait la figure 21.4, ma consommation de gaz a chuté de 40 kWh/j à 13 kWh/j — c’est-à-dire une réduction de 67 %.

Tableau E.9. Analyse des réductions prévues de pertes de chaleur dans ma maison, durant une froide journée d’hiver.

– Isolation des murs creux (applicable aux deux tiers de la surface des murs)	4,8 kWh/d
– Amélioration de l’isolation du toit	3,5 kWh/d
– Réduction de la conduction en passant en double vitrage deux portes et une fenêtre	1,9 kWh/d
– Réduction de la ventilation du couloir et de la cuisine en améliorant les portes et les fenêtres	2,9 kWh/d

Réduire les déperditions par des revêtements muraux intérieurs

Est-ce que vous pouvez réduire la déperdition de vos murs en couvrant leur intérieur avec un isolant ? La réponse est oui, mais il peut y avoir deux complications. Tout d’abord, l’épaisseur du revêtement intérieur est supérieure à ce que vous pourriez imaginer. Pour transformer un mur de 23 cm d’épaisseur construit en brique pleine (coefficient U de 2,2 W/m²/K) en un mur décemment isolé à 0,3 W/m²/K, il faut ajouter environ 6 cm de panneau isolant [65h3cb]. Par ailleurs, de la condensation peut apparaître sur la face intérieure de ces couches isolantes, provoquant des problèmes d’humidité.

Si vous ne cherchez pas à atteindre une réduction aussi importante de la déperdition de vos murs, vous pouvez vous en sortir avec un isolant plus mince. Par exemple, vous pouvez acheter des panneaux muraux isolants épais de 1,8 cm avec un coefficient U de 1,7 W//m²/K. Recouvrir votre mur de tels panneaux réduira son coefficient U, le faisant passer de 2,2 W//m²/K à :

Sans aucun doute, une réduction digne d’intérêt.

L’échange d’air

Une fois un bâtiment vraiment bien isolé, les principales pertes de chaleur proviennent de la ventilation (c’est-à-dire du renouvellement de l’air) plutôt que de la conduction. La chaleur perdue par ventilation peut être réduite en transférant la chaleur de l’air sortant à l’air entrant. De façon tout à fait remarquable, une bonne partie de cette chaleur peut effectivement être transférée sans avoir besoin d’aucune énergie additionnelle. L’astuce consiste à utiliser un nez, comme l’a découvert la sélection naturelle. Un nez réchauffe l’air entrant en refroidissant l’air sortant. Il y a un gradient de température le long du nez ; les murs du nez sont les plus froids à proximité des narines. Plus votre nez est long, mieux il fonctionne comme un échangeur de chaleur à contre-courant. Dans les nez naturels, la direction du flux d’air est généralement alternée. Une autre façon de concevoir un nez est d’avoir deux voies aériennes, une pour le flux entrant, et une pour le flux sortant, séparées du point de vue de l’air, mais étroitement accolées l’une à l’autre afin que la chaleur puissent aisément s’écouler entre les deux conduits. C’est ainsi que fonctionnent les nez dans les bâtiments. Par convention, on appelle ces nez des échangeurs de chaleur.

Une maison économe en énergie

Figure E.10. La maison « Heatkeeper » Serrekunda.

En 1984, un consultant en énergie, Alan Foster, a construit une maison économe en énergie près de Cambridge ; il m’a aimablement donné ses mesures détaillées. La maison est un bungalow à charpente en bois basée sur une conception scandinave appelée « Heatkeeper Serrekunda » (figure E.10) ; elle a une surface au sol de 140 m², et comprend trois chambres, un bureau, deux salles de bains, un salon, une cuisine et un vestibule. Les murs extérieurs en bois ont été fournis en kit par une société écossaise, et il a suffi de quelques jours pour assembler le gros oeuvre de la maison. Avec leurs 30 centimètres d’épaisseur, les murs ont un coefficient U de 0,28 W/m²/°C. De l’intérieur à l’extérieur, ils sont constitués d’un panneau de Placoplatre de 13 mm d’épaisseur, d’une couche d’air de 27 mm, d’une couche de protection contre la condensation, de 8 mm de contre-plaqué, de 90 mm de laine de roche, de 12 mm de panneau de fibre de bois imprégnée de bitume, de 50 mm creux, et de 103 mm de brique. La construction du plafond est similaire, à ceci près que l’on y a ajouté entre 100 et 200 mm d’isolation avec de la laine de roche. Le plafond a un coefficient U de 0,27 W/m²/°C, et le plancher, 0,22 W/m²/°C. Les fenêtres sont en double vitrage (coefficient U de 2 W/m²/°C), avec un traitement spécial de la surface extérieure du vitrage intérieur de façon à réduire le rayonnement de chaleur. Les fenêtres sont disposées de façon à apporter un gain solaire substantiel, et contribuer ainsi à environ 30 % de l’apport en chauffage de la maison.

Figure E.11. L’échangeur de chaleur de la maison Heatkeeper.

La maison est bien calfeutrée, chaque porte et chaque fenêtre étant bordée d’un joint en néoprène. La maison est chauffée par de l’air chaud pompé à travers des grilles dans le sol ; en hiver, les pompes retirent l’air usagé de plusieurs pièces, le rejetant à l’extérieur, et prenant l’air dans le grenier. L’air entrant et l’air sortant traversent un échangeur de chaleur (figure E.11), qui récupère 60 % de la chaleur dans l’air sortant. L’échangeur de chaleur est un système passif, qui ne consomme pas d’énergie ; c’est comme un grand nez en métal, qui réchauffe l’air entrant avec l’air sortant. Un jour d’hiver vraiment froid, où la température extérieure était de −8°C, la température au niveau de la prise d’air du grenier était de 0°C, et l’air sortant de l’échangeur de chaleur était à +8°C.

Pendant les dix premières années, la chaleur provenait entièrement de radiateurs électriques, chauffant une réserve de chaleur de 600 litres la nuit pendant les heures creuses. Plus récemment, la maison a été reliée au gaz de ville, et le chauffage de la maison provient maintenant d’une chaudière à condensation.

Les pertes de chaleur par conduction et ventilation se montent à 4,2 kWh/j/°C. Le paramètre de pertes thermiques (la déperdition par mètre carré de surface au sol) est de 1,25 W/m²/°C (à comparer avec celui de ma maison : 2,7 W/m²/°C).

La maison étant occupée par deux personnes, la consommation de chauffage moyenne, avec un thermostat réglé à 19 ou 20°C durant la journée, était de 8 100 kWh par an, soit 22 kWh/j ; la consommation énergétique totale tous usages confondus était d’environ 15 000 kWh par an, soit 40 kWh/j. Exprimée sous la forme d’une puissance moyenne par unité de surface, cela fait 6,6 W/m² pour le chauffage et 12,2 W/m² au total.

La figure E.12 compare la consommation de puissance par unité de surface de cette maison « Heatkeeper » avec celle de ma propre maison (avant et après mes améliorations) et avec la moyenne européenne. La consommation de ma maison après améliorations est proche de celle de la maison « Heatkeeper », grâce à mon thermostat réglé à un niveau plus bas.

Références pour les maisons et les bureaux

Le standard allemand de Maison passive vise une consommation énergétique pour le chauffage et le refroidissement de 15 kWh/m² par an, soit une densité moyenne de puissance de 1,7 W/m² ; et une consommation énergétique totale de 120 kWh/m² par an, soit 13,7 W/m² en moyenne.

La consommation de puissance moyenne du secteur des services dans le Royaume-Uni, par unité de surface au sol, est de 30 W/m²..

Un bureau économe en énergie

La National Energy Foundation britannique s’est construit un bâtiment à faible coût et faible consommation d’énergie. Ce dernier possède des panneaux solaires pour l’eau chaude, des panneaux photovoltaïques qui génèrent jusqu’à 6,5 kW d’électricité, et il est chauffé par une pompe à chaleur géothermique et de temps en temps par un poêle à bois. Sa surface au sol est de 400 m², pour environ 30 occupants. C’est un bâtiment à un seul étage. Les murs contiennent 300 mm d’isolation par laine de roche. Le coefficient de performance de la pompe à chaleur en hiver est de 2,5. L’énergie consommée est de 65 kWh par an par m² de surface (7,4 W/m²), dont environ 20 % sont produits par le système photovoltaïque.

Bureaux contemporains

On vante fréquemment les qualités environnementales fantastiques des immeubles de bureaux de construction très récente. Jetons un coup d’oeil sur quelques chiffres les concernant.

Le bâtiment William Gates de l’université de Cambridge abrite des chercheurs en informatique, des administratifs, et un petit café. Sa surface est de 11 110 m², et il consomme 2 392 MWh/an d’énergie. Cela fait une puissance par unité de surface de 215 kWh/m²/an, soit 25 W/m². Ce bâtiment a remporté un prix RIBA en 2001 pour sa consommation énergétique prévue. « Les architectes ont incorporé de nombreux éléments améliorant l’impact environnemental dans le bâtiment ». [5dhups]

Mais faut-il vraiment se laisser impressionner par ces bâtiments ? Juste à côté, l’immeuble Rutherford, construit pendant les années 1970 sans aucune prétention écologique — il n’a même pas de double vitrage — fait 4 998 m² et consomme 1 557 MWh par an ; ce qui fait 0,85 kWh/j/m², ou 36 W/m². Autrement dit, en puissance consommée par unité de surface, l’immeuble primé n’est que 30 % meilleur que son cousin basique des années 70. La figure E.12 compare ces bâtiments et un autre bâtiment récent, celui de la Faculté de Droit, aux Vieilles écoles, qui sont d’anciens bureaux construits avant 1890. Malgré les annonces en fanfare, la différence entre le récent et l’ancien est en fait bien décevante !

Figure E.12. Comparaisons de bâtiments. Puissance consommée par unité de surface dans divers bureaux et habitations.1

Figure E.13. Rendements de pompes à chaleur idéales.
En haut à gauche : l’énergie électrique qui serait nécessaire dans l’idéal, selon les limites de la thermodynamique, pour pomper de la chaleur en dehors d’un endroit à la température T_int, quand la chaleur est pompée à un endroit à la température T_ext = 35°C.
À droite : l’énergie électrique qui serait nécessaire dans l’idéal pour pomper de la chaleur vers un endroit à la température T_int, quand la chaleur est pompée depuis un endroit à la température T_ext = 0°C.
Ligne du bas : par convention, le rendement est exprimé sous forme d’un « coefficient de performance », qui représente la chaleur pompée par unité d’énergie électrique. En pratique, à ce que j’ai compris, les pompes à chaleur géothermiques bien installées et les meilleures pompes à chaleur air-air ont généralement un coefficient de performance de 3 ou 4 ; cependant, les règlements gouvernementaux au Japon ont poussé le coefficient de performance jusqu’à 6,6.

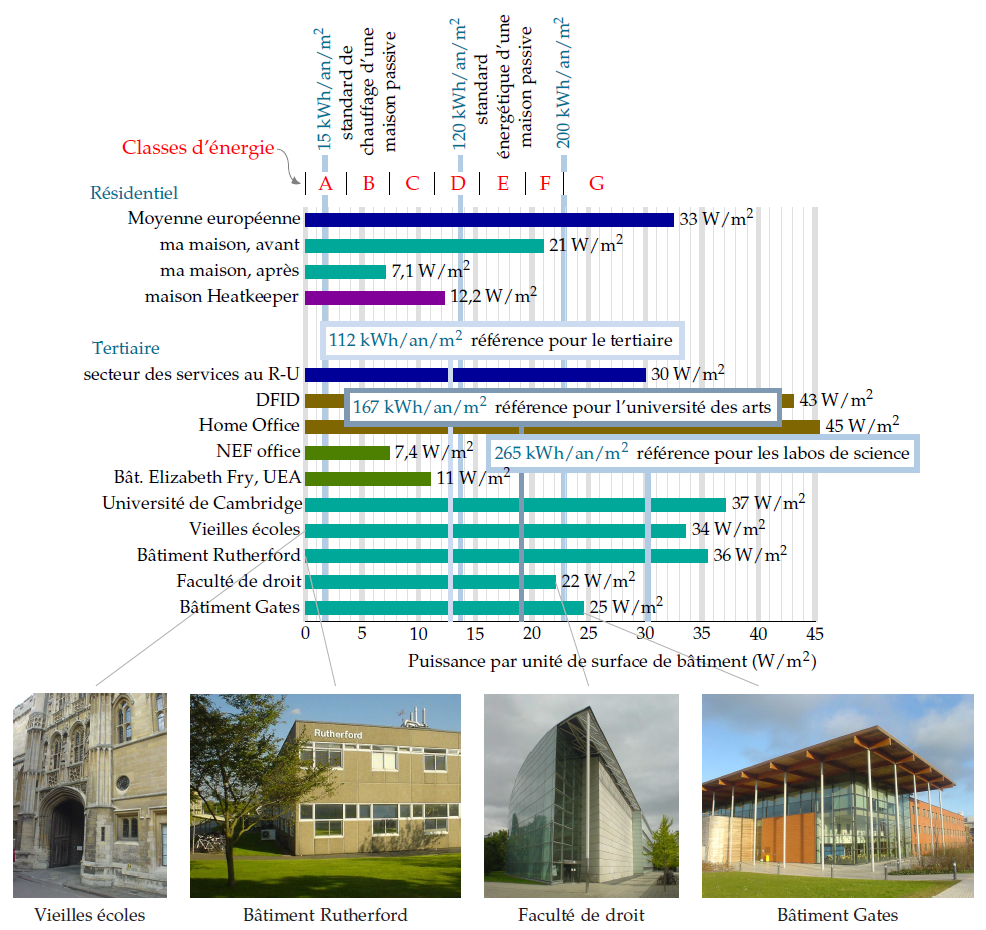
Remarquez que les consommations de puissance des bâtiments, par unité de surface, sont exprimées exactement dans les mêmes unités (W/m²) que les productions par unité de surface d’énergie renouvelable que nous avons décrites pages 52, 55 et 209. Mettre côte à côte ces consommations et les chiffres pour la production permet de prendre conscience à quel point alimenter des bâtiments modernes intégralement avec des énergies renouvelables produites sur place est difficile. La puissance par unité de surface des biocarburants (figure 6.12) est de 0,5 W/m² ; celles des fermes éoliennes, de 2 W/m² ; celle du photovoltaïque, de 20 W/m² (figure 6.18) ; seuls les panneaux solaires thermiques nous amènent à peu près dans la bonne gamme de densités de puissance : 53 W/m² (figure 6.3).

Améliorer le coefficient de performance

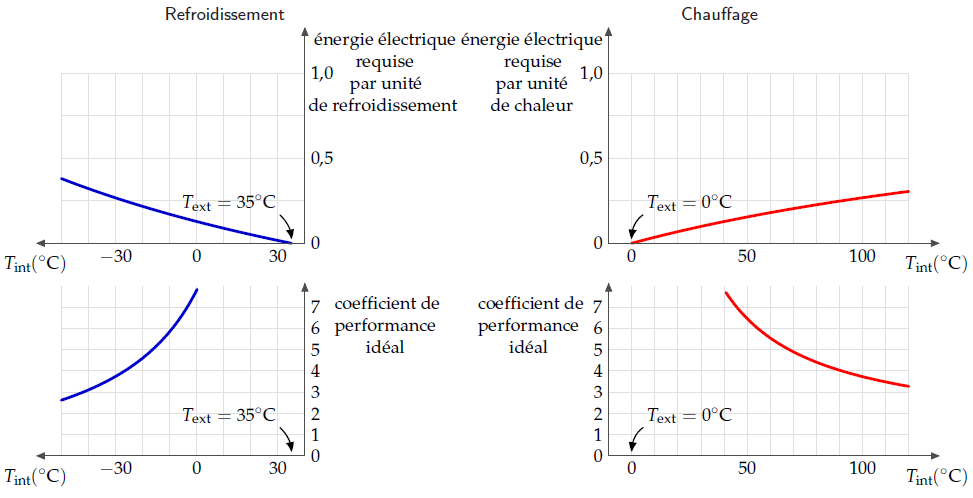
Vous avez peut-être l’impression que le coefficient de performance d’une chaudière à condensation, qui est de 90 %, sera difficile à battre. Mais on peut nettement l’améliorer avec des pompes à chaleur. Tandis que la chaudière à condensation utilise de l’énergie chimique et en transforme 90 % en chaleur utile, la pompe à chaleur utilise de l’énergie électrique et s’en sert pour déplacer de la chaleur d’un endroit à un autre (par exemple, de l’extérieur à l’intérieur d’un bâtiment). En général, la quantité de chaleur utile fournie est largement supérieure à la quantité d’électricité consommée. Un coefficient de performance de 3 ou 4 est quelque chose de tout à fait normal.

La théorie des pompes à chaleur

Voici les formules qui donnent le rendement idéal d’une pompe à chaleur, c’est-à-dire la quantité d’énergie électrique requise par unité de chaleur pompée. Si l’on pompe de la chaleur à partir d’une zone extérieure à la température T₁ vers une zone à une température supérieure T₂, les deux températures étant exprimées par rapport au zéro absolu (autrement dit, T₂, en kelvins, se déduit de la température en degrés Celsius T_int en y ajoutant 273,15), le rendement idéal est égal à :

Si l’on pompe de la chaleur hors d’un endroit à la température T₂ vers un extérieur plus chaud à la température T₁, le rendement idéal est égal à :

Ces limites théoriques ne peuvent être atteintes que par des systèmes qui pomperaient la chaleur de façon infiniment lente. Remarquez que plus la température intérieure T₂ est proche de la température extérieure T₁, plus le rendement idéal est élevé.

Bien que, en théorie, des pompes à chaleur exploitant la chaleur du sol puissent avoir une meilleure performance que celles utilisant la chaleur de l’air, puisque la température du sol est en général plus proche de la température intérieure que celle de l’air, en pratique une pompe à chaleur air-air pourrait bien constituer le meilleur et le plus simple des choix. Dans les grandes villes, il n’est pas sûr que le choix des pompes à chaleur sol-air soit le plus judicieux à long terme, car plus les gens qui s’en servent en hiver sont nombreux, plus le sol devient froid ; ce problème de décharge thermique sauvage pourrait aussi apparaître en été dans les villes où un trop grand nombre de bâtiments auraient recours à des pompes à chaleur sol-air (ou devrais-je dire « puits-air » ?) pour la climatisation.

Le chauffage et le sol

Capacité calorifique :	C = 820 J/kg/K
Conductivité :	κ = 2,1 W/m/K
Densité :	ρ = 2 750 kg/m³
Capacité calorifique par unité de volume :
	C_V = 2,3 MJ/m³/K

Tableau E.14. Statistiques fondamentales du granite (j’ai pris le granite comme exemple de roche typique).

Voici un calcul intéressant à faire. Imaginez que vous ayez des panneaux solaires thermiques sur votre toit et que, dès que l’eau dans les panneaux dépasse les 50°C, vous pompiez l’eau à travers un gros rocher sous votre maison. Quand arrivent les mois gris, mornes et froids, vous pourriez alors utiliser la chaleur contenue dans ce rocher pour chauffer votre maison. En gros, quelle taille devrait avoir un rocher à 50°C pour stocker assez de chaleur pour chauffer une maison pendant un mois entier ? Supposons que l’on souhaite obtenir 24 kWh par jour pendant 30 jours et que la maison soit à 16°C. La capacité calorifique du granite est égale à 0,195 × 4 200 J/kg/K = 820 J/kg/K. La masse de granite nécessaire est donc égale à :

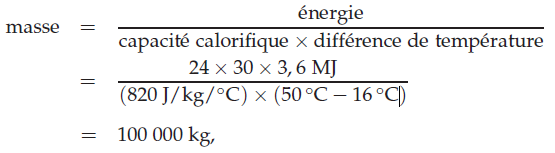
soit 100 tonnes, ce qui correspond à un rocher en forme de pavé, d’une taille de 6 m × 6 m × 1 m.

Stockage dans le sol sans paroi

(W/m/K)
eau	0,6
quartz	8
granite	2,1
croûte terrestre	1,7
terre sèche	0,14

Tableau E.15. Conductivités thermiques. Pour plus de données, voir le tableau E.18.

OK, nous avons déterminé la taille d’une réserve utile dans le sol. Mais est-il difficile de conserver la chaleur ? Aurait-on besoin d’envelopper notre rocher en forme de très gros pavé d’une épaisse couche isolante ? En fait, il s’avère que le sol lui-même est un assez bon isolant. Un pic de chaleur envoyé dans un trou dans le sol s’y diffusera selon la formule :

où κ est la conductivité du sol, C sa capacité calorifique, et ρ sa densité. Cette expression décrit une courbe en cloche de largeur égale à :

par exemple, après six mois (t = 1,6 × 10⁷ s), en utilisant les valeurs du granite (C = 0,82 kJ/kg/K, ρ = 2 500 kg/m³, κ = 2,1 W/m/K), la largeur est de 6 mètres.

En utilisant les chiffres pour l’eau (C = 4,2 kJ/kg/K, ρ = 1 000 kg/m³, κ = 0,6 W/m/K), la largeur est de 2 mètres.

Donc si la zone de stockage est plus grande que 20 m × 20 m × 20 m alors la majorité de la chaleur stockée y sera toujours six mois plus tard (car 20 mètres sont significativement plus grands que 6 mètres et 2 mètres).

Les limites des pompes à chaleur géothermiques

La faible conductivité thermique du sol est à double tranchant. Grâce à sa faible conductivité, le sol retient bien la chaleur pendant longtemps. Mais par ailleurs, cette faible conductivité signifie qu’il n’est pas facile de déplacer rapidement de la chaleur vers et en provenance du sol. Explorons maintenant de quelle façon la conductivité du sol limite l’utilité des pompes à chaleur géothermiques.

Considérons un quartier avec une densité de population vraiment élevée. Est-ce que tout le monde peut utiliser des pompes à chaleur géothermiques, sans avoir recours à un remplacement actif en été (tel que décrit en page 181) ? Le souci vient du fait que si nous aspirons tous de la chaleur du sol en même temps, on pourrait faire geler le sol. Je vais traiter cette question avec deux calculs. En premier lieu, je vais calculer à combien se montent les flux naturels d’énergie qui vont vers le sol et en repartent, en été et en hiver.

Figure E.16. La température à Cambridge, en 2006, et un schéma, qui nous donne la température comme la somme d’une variation annuelle sinusoïdale entre 3°C et 20°C, et d’une variation sinusoïdale quotidienne avec un intervalle jusqu’à 10,3°C. La température moyenne est 11,5°C.

Si le flux que nous voulons aspirer du sol en hiver est bien plus élevé que ces flux naturels, alors nous saurons que notre aspiration va altérer de manière significative les températures du sol, et donc qu’elle pourrait ne pas être faisable. Pour ce calcul, je vais supposer que le sol qui se trouve juste sous la surface est maintenu, par les influences combinées du soleil, de l’air, des nuages et du ciel nocturne, à une température qui augmente et diminue lentement pendant l’année (figure E.16).

La réponse aux variations de température extérieure

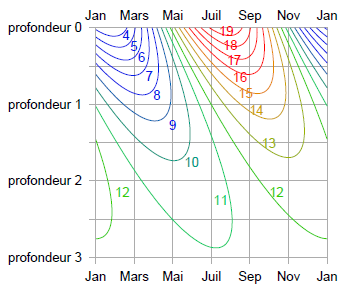
Figure E.17. La température (en°C) en fonction de la profondeur et du temps. Les profondeurs sont indiquées en un multiple de la dimension caractéristique z₀, qui, pour le granite et des variations annuelles, est de 3 mètres.
À une « profondeur 2 » (6 mètres), la température est toujours environ 11 ou 12°C. À une « profondeur 1 » (3 mètres), elle oscille entre 8 et 15°C.

Pour établir la réponse de la température dans le sol par le calcul, et pour déterminer quel est le flux entrant ou sortant, il faut un peu de mathématiques avancées, que j’ai rassemblées dans le cadre E.19.

On est récompensé de tous ces calculs par un fort beau diagramme (figure E.17) qui indique comment la température varie dans le temps à chaque profondeur. Ce diagramme montre la réponse de n’importe quel matériau en prenant comme unité sa dimension caractéristique z₀ (équation E.7), qui dépend de la conductivité du matériau κ et de sa capacité calorifique C_V, ainsi que de la fréquence des variations de température extérieure ω. (Avec la même théorie, on peut choisir de considérer soit les variations quotidiennes, soit les variations annuelles). A une profondeur de 2 z₀, les variations en température ont une amplitude d’un septième de celles en surface, et sont en retard sur celle-ci d’environ un tiers de cycle (figure E.17). A une profondeur de 3 z₀, les variations de température ne valent plus qu’un vingtième de celles en surface, et sont décalées d’un demi-cycle.

Dans le cas des variations quotidiennes et du granite bien dur, la dimension caractéristique est de z₀ = 0,16 m. (Il vous donc faut une épaisseur de roche de 32 cm pour dompter les oscillations de température quotidiennes). Pour des variations annuelles et avec du granite, la dimension caractéristique est de z₀ = 3 m.

Concentrons-nous sur les variations annuelles ; ensuite, nous parlerons de deux ou trois autres choses. Les dimensions caractéristiques pour divers matériaux sont indiquées dans la troisième colonne du tableau E.18. Pour des sols sableux humides ou pour du béton, la dimension caractéristique z₀ est similaire à celle du granite — environ 2,6 m. Avec des sols secs ou tourbeux, la dimension caractéristique z₀ est plus courte — environ 1,3 m. Cela semble une bonne nouvelle, car cela signifie que vous n’aurez pas besoin de creuser aussi profond pour atteindre un terrain avec une température stable. Mais cela s’accompagne d’une mauvaise nouvelle : les flux naturels sont plus faibles dans les sols secs.

Les flux naturels varient au cours de l’année ; plus la conductivité est faible, plus la valeur maximale qu’ils atteignent est basse (équation E.9). Dans le cas du granite, le flux maximal s’élève à 8 W/m². Pour des sols secs, le flux maximal va de 0,7 W/m² à 2,3 W/m². Pour des sols humides, le flux maximal va de 3 W/m² à 8 W/m².

Qu’est-ce que cela implique ? Je suggère que nous prenions comme référence utile un flux dans la moyenne de ces valeurs, disons 5 W/m², ce qui nous donne une indication sur l’ordre de grandeur de la puissance que l’on peut espérer extraire, par unité de surface, avec une pompe à chaleur géothermique. Si l’on aspire un flux nettement plus faible que 5 W/m², la perturbation que nous ajouterons aux flux naturels sera petite. Si, au contraire, on essaie d’aspirer un flux plus élevé que 5 W/m², alors il faut s’attendre à faire dévier de manière significative la température du sol de sa valeur naturelle ; dans la durée, de tels flux pourraient bien s’avérer impossibles à maintenir.

Tableau E.18. Conductivité thermique et capacité calorifique de différents matériaux et types de sol, accompagnés de la dimension caractéristique z₀ = √2κ/(C_Vω) et du flux maximal A√C_Vκω associés à des variations de température annuelle d’amplitude A = 8,3°C qui correspondent à ces matériaux et types de sol. Les sols sableux et argileux ont une porosité de 0,4 ; le sol tourbeux une porosité de 0,8.2

	conductivité thermique κ (W/m/K)	capacité calorifique C_V (MJ/m³/K)	dimension caractérist. z₀ (m)	flux A√C_Vκω (W/m²)
Air	0,02	0,0012
Eau	0,57	4,18	1,2	5,7
Granite	2,1	2,3	3,0	8,1
Béton	1,28	1,94	2,6	5,8

Sol sableux
Sec	0,30	1,28	1,5	2,3
Saturé à 50 %	1,80	2,12	2,9	7,2
Saturé à 100 %	2,20	2,96	2,7	9,5

Sol argileux
Sec	0,25	1,42	1,3	2,2
Saturé à 50 %	1,18	2,25	2,3	6,0
Saturé à 100 %	1,58	3,10	2,3	8,2

Sol tourbeux
Sec	0,06	0,58	1,0	0,7
Saturé à 50 %	0,29	2,31	1,1	3,0
Saturé à 100 %	0,50	4,02	1,1	5,3

La densité de population d’une banlieue anglaise typique correspond à 160 m² par personne (rangées de maisons mitoyennes avec environ 400 m² par maison, en incluant les trottoirs et les rues). Avec une telle densité d’espace résidentiel, on peut en déduire à la louche que la limite du débit des pompes à chaleur est de :

5 W/m² × 160 m² = 800 W = 19 kWh/j par personne.

Voilà qui est désagréablement proche du niveau de puissance que l’on aimerait pouvoir fournir en hiver ; pour une maison ancienne comme la mienne, il est vraisemblable que la demande hivernale maximale en air chaud et en eau chaude soit de 40 kWh/j par personne.

Ce calcul suggère que dans une banlieue typique, tout le monde ne peut pas utiliser des pompes à chaleur géothermiques, à moins de faire attention à renvoyer la chaleur dans le sol de façon active pendant l’été.

Faisons un second calcul pour déterminer la quantité de puissance que l’on pourrait aspirer en continu d’une boucle dans le sol à une profondeur de h = 2 m. Supposons que l’on se permette d’aspirer la température au niveau de la boucle jusqu’à atteindre ΔT = 5°C en dessous de la température moyenne du sol à la surface, et supposons qu’en surface, la température soit constante. On peut alors en déduire le flux de chaleur depuis la surface. En prenant une conductivité de 1,2 W/m/K (typique d’un sol argileux humide) :

Si, comme précédemment, on fait l’hypothèse d’une densité de population de 160 m² par habitant, alors la puissance maximale par personne que peuvent fournir des pompes à chaleur géothermiques, si tout le monde en a dans le quartier, est de 480 W, ce qui fait 12 kWh/j par personne.

On arrive donc encore une fois à la conclusion que dans une banlieue typique composée de maisons mal isolées comme la mienne, tout le monde ne peut pas utiliser des pompes à chaleur géothermiques, à moins de bien veiller à recharger le sol en chaleur pendant l’été. Et dans les villes avec des densités de population plus élevées, les pompes à chaleur géothermiques ne sont probablement pas une solution viable.

Par conséquent, je suggère les pompes à chaleur air-air comme meilleur choix de chauffage pour le plus grand nombre.

L’inertie thermique

Peut-on réduire sa facture de chauffage et de rafraîchissement en augmentant l’inertie thermique d’un bâtiment ? Cela dépend. La température extérieure peut varier d’environ 10°C sur une journée. Un bâtiment avec une inertie thermique élevée — avec d’épais murs de pierre de taille, par exemple — atténuera naturellement ces variations de température, et, sans chauffage ni refroidissement, aura une température proche de la température moyenne à l’extérieur. Ces bâtiments, au Royaume-Uni, n’ont besoin ni de chauffage ni de climatisation de nombreux mois de l’année. Au contraire, un bâtiment mal isolé et avec une faible inertie thermique pourra sembler trop chaud le jour et trop froid la nuit, conduisant à une plus forte dépense de climatisation et de chauffage.

Cependant, une inertie thermique élevée n’est pas toujours la panacée. Si une pièce n’est occupée en hiver que quelques heures par jour (prenez une salle de lecture, par exemple), le coût énergétique pour réchauffer cette pièce à une température confortable sera d’autant plus grand que l’inertie thermique de la pièce est grande. Cette chaleur dépensée en plus restera plus longtemps dans une pièce thermiquement massive, mais si personne n’est là pour en profiter, cette chaleur est gaspillée. Donc, dans le cas de pièces peu utilisées, il est plus logique de concevoir une structure à faible inertie thermique, que l’on chauffera rapidement au moment où on en aura besoin.

Cadre E.19. Calcul du flux naturel provoqué par des variations de température sinusoïdales.

Supposons que le sol soit constitué d’un matériau solide et homogène, de conductivité κ et de capacité calorifique C_V. La température à la profondeur z et au temps t répond alors à la température imposée à la surface selon l’équation de diffusion :

(E.4)

Pour une température imposée de forme sinusoïdale, de fréquence ω et d’amplitude A à la profondeur z = 0,

T(0, t) = T_surface(t) = T_moyenne + A cos(ωt),

(E.5)

la température résultante à la profondeur z et au temps t est une fonction décroissante et oscillante :

T(z, t) = T_moyenne(t) + A e^-z/z₀ cos(ωt − z/z₀),

(E.6)

où z₀ est la dimension caractéristique à la fois de la décroissance et de l’oscillation,

(E.7)

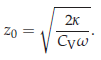
Le flux de chaleur (puissance par unité de surface) à la profondeur z est égal à :

(E.8)

Par exemple, à la surface, le flux maximal est égal à :

(E.9)

Notes et bibliographie

^↑ 1 Figure E.12. Les normes de Maison Passive utilisent une convention différente de celle de ce livre pour définir la puissance, en la mesurant en termes de « consommation d’énergie primaire ». Cela impose donc de connaître la manière dont sont obtenus l’électricité et les combustibles consommés, ainsi que les facteurs de conversion énergétique utilisés. Cela signifie aussi que les normes de Maison Passive sont en réalité plus sévères que ce que ne suggère cette figure (quant à savoir à quel point ces normes sont plus sévères, cela dépend du mix énergétique utilisé). Soit dit en passant, si la Maison Passive consomme 6,6 W/m² pour la puissance calorifique et 12,2 W/m² en tout, l’analyse de la consommation de ma propre maison « après », montre une consommation de 6,2 W/m² de gaz et de 7,1 W/m² en tout.

^↑ 2 Tableau E.18. Sources : Bonan (2002), www.hukseflux.com/thermalScience/thermalConductivity.html